Sommaire de cette fiche
I. Inégalité triangulaire.
1. Distance entre trois points.
On considère trois points A,B et C. Si le point B n’appartient pas au segment [AC], alors on l’inégalité 
.
Exemple :
Dans la figure ci-dessous, le point B n’appartient pas au segment [AC].
On a l’égalité .
et
on a bien .
.png)
On considère trois points A, B et C.
Si le point B appartient au segment [AC] alors on a l’égalité .
Exemple :
Dans la figure ci-dessous, le point B appartient au segment [AC].
Nous avons l’égalité .
2. Inégalité triangulaire.
Si A,B et C désignent trois points quelconques alors on a l’inégalité .
Pour les triangles, on a alors la conséquence suivante :
Dans un triangle (non aplati), la longueur de chaque côté est inférieure à la somme des longueurs des deux autres côtés.
Remarque :
La distance la plus courte est toujours la ligne droite.
Exemple :
Dans le triangle PSG ci-dessous, on a les trois inégalités :
.png)
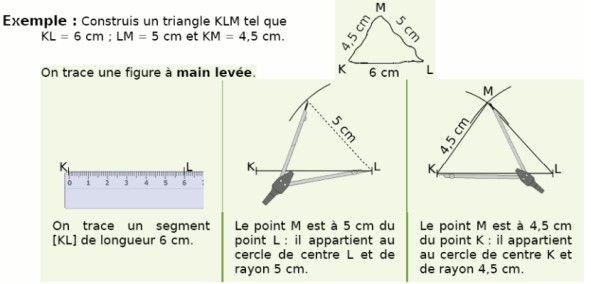
II. Construire un triangle.
1. Construire un triangle avec une règle et un compas.
Trois longueurs étant données, si la plus grande longueur est inférieure ou égale à la somme des deux autres, alors on peut construire un triangle dont les côtés mesurent ces trois longueurs.
Dans le cas contraire, le triangle n’est pas constructible.
Méthode :
- On compare la plus grande longueur et la somme des deux autres longueurs (application de l’inégalité triangulaire);
- On interprète la comparaison;
- On conclut;
- On construit le triangle.
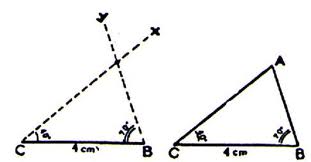
2.Construire un triangle avec une règle et un rapporteur.
Méthode :
Pour construire un triangle connaissant deux côtés et l’angle compris entre ces deux côtés.
.jpg)
Méthode :
Pour construire un triangle connaissant un côté et les deux angles adjacents à ce côté.
III. Cercle circonscrit à un triangle.
1. Médiatrices d’un triangle.
Les trois médiatrices des côtés d’un triangle (non aplati) sont concourantes.
2. Cercle circonscrit à un triangle.
Le cercle circonscrit à un triangle est le cercle qui passe par les trois sommets du triangle.
Le centre du cercle circonscrit à un triangle est le point de concours des médiatrices des côtés de ce triangle.
