La bissectrice d’un angle avec des exercices de maths en 6ème corrigés pour réviser ses chapitres. Ces fiches sont à imprimer en PDF. L’élève devra être capable de construire la bissectrice d’un angle avec le rapporteur ou avec le compas et sa règle en sixième.
Exercice 1 – Construire la bissectrice d’un angle donné
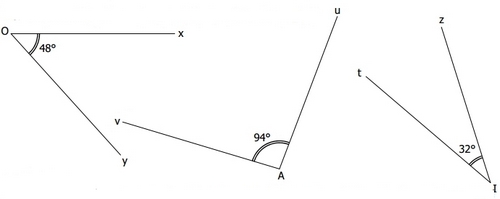
Dans chaque cas, tracer un angle de la mesure indiquée
et construire sa bissectrice avec la règle et le rapporteur.
Exercice 2 – Angles et bissectrices
1. Tracer un angle de
.
Construire sa bissectrice (d) avec la règle et le compas.
2. On note K le point d’intersection de la droite (d) et du segment [IJ].
Mesurer les angles et
avec le rapporteur.
Le résultat était-il prévisible ?
Exercice 3 – Construction d’un triangle et des bissectrices
Tracer un triangle EFG et construire avec la règle et le compas la bissectrice
de chacun des angles de ce triangle.
Exercice 4 – Tracer un angle et construire la bissectrice
Dans chaque cas, tracer un angle de la mesure indiquée
et construire sa bissectrice avec la règle et le compas.
Exercice 5 – Construction des bissectrices d’un triangle
Soit ABC un triangle tel que AB = 6 cm, AC = 4 cm et BC= 7 cm.
Construire les bissectrices des trois angles de ce triangle.
Exercice 6 – Construction de la bissectrice d’un angle
Construire à l’aide votre rapporteur les bissectrices de ces trois angles.




 Mathovore c'est 13 931 505 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 931 505 cours et exercices de maths téléchargés en PDF.