Exercice 1 :
Dériver la fonction f dans les cas suivants :
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Exercice 2 :
Determiner une equation de la tangente T à la courbe representative de la fonction f au point d’abscisse a dans les cas suivants :
1. f(x)= 3x²-x+1 avec a= -1.
2. avec a= 3.
3. avec a= 9.
Exercice 3 :
Soit f la fonction définie sur par :
.
On note C sa courbe representative dans un repère orthonormé .
1. Determiner les abscisses des points de la courbe C où la tangente est horizontale .
2. Existe-t-il des points de la courbe C où la tangente admet un coefficient directeur égal à – 2 ?
3 Determiner les abscisses des points de la courbe C où la tangente est parallèle à la droite d’équation .
Exercice 4 – Equation de la tangente à une courbe représentative
Soit f la fonction définie sur R par .
Soit (Cf ) sa courbe représentative.
1. Donner, en justifiant, l’équation de la tangente (T) à la courbe (Cf ) au point A d’abscisse 0.
2. Tracer dans un même repère la courbe (Cf ) et la tangente (T) sur l’intervalle [- 1 ; 1,5].
Exercice 5 – Calculer une limite
Le but de cet exercice est de calculer la limite suivante :
.
Pour cela on considère la fonction définie sur
par
.
1. Calculer la dérivée f’ de la fonction f. Calculer f ‘ (0).
2. Calculer l’accroissement moyen de la fonction f entre 0 et h. En déduire la limite ci-dessus.
Exercice 6 – Prix de revient et vitesse d’un camion
Un camion doit faire un trajet de 150 km.
Sa consommation de gasoil est de llitres par heure, où
désigne sa vitesse en
.
Le prix du gasoil est de 0,9 € le litre et on paie le chaufeur 12 € par heure.
1. Soit t la durée du trajet en heure. Exprimer t en fonction de la vitesse .
2. Calculer le prix de revient P(v) du trajet en fonction de v.
3. Quel doit être la vitesse v du camion pour que le prix de revient P(v) de la course soit minimal ?
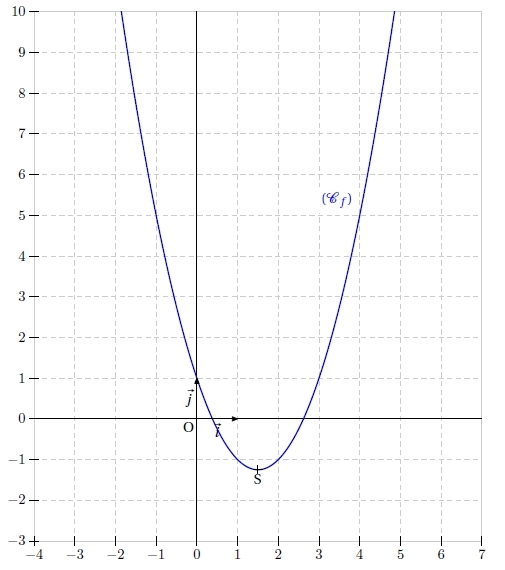
Exercice 7 – Sommet d’une parabole
Soit (P) la parabole définie par la fonction .
Calculer les coordonnées de son sommet S.
Exercice 8 – Etude d’un rectangle
On considère un rectangle dont le périmètre P est égal à 4 cm.
1. Déterminer ses dimensions (longueur L et largeur l) sachant que son aire S est égale à cm².
2. On recherche maintenant les dimensions du rectangle de façon que son aire S soit maximale.
a. Exprimer S en fonction de la largeur l.
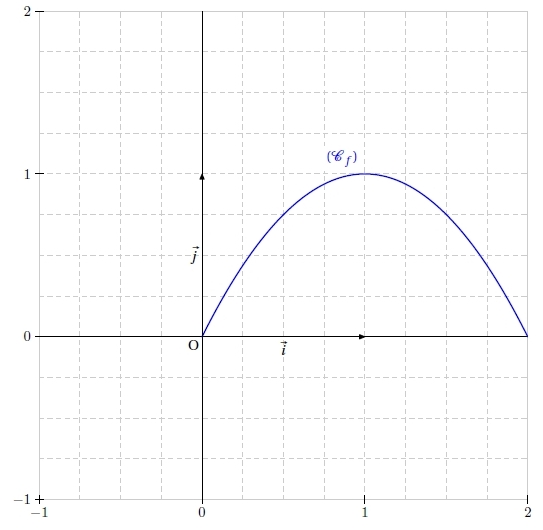
b. On considère la fonction f définie sur par
.
Calculer la dérivée f’ de f puis étudier son signe.
Dresser le tableau de variations de la fonction f.
Tracer la représentation graphique (Cf ) de la fonction f sur [0 ; 2].
c. En déduire les dimensions du rectangle dont le périmètre P est égal à 4 m et l’aire S est maximale.
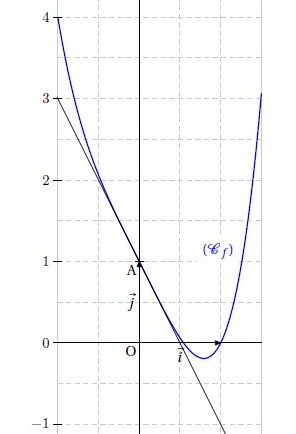
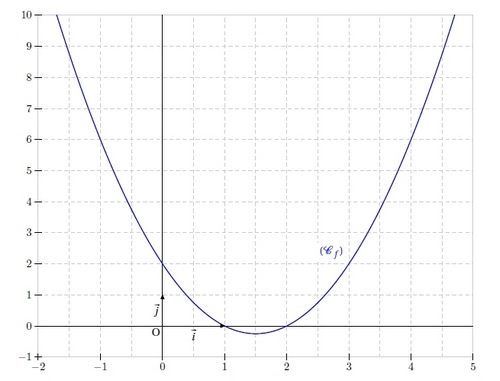
Exercice 9 – Fonction numérique et racine
On considère la fonction f définie sur R par : .
On note (Cf ) sa représentation graphique.
1.Calculer la dérivée f ‘ de f puis étudier son signe.
2. Dresser le tableau de variations de la fonction f.
3. Déterminer une équation de la tangente (T) à (Cf ) au point d’abscisse 0.
4. Tracer (T) et (Cf ) dans un même repère.
5. Démontrer que l’équation f(x) = 0 admet une solution unique dans l’intervalle [2 ; 3].
6. Donner une valeur approchée de , par défaut, à
près.
Exercice 10 – Tableau de variation et équation
1. Dresser le tableau de variations de la fonction f définie sur R par :
2. Résoudre l’équation f(x) = 0.
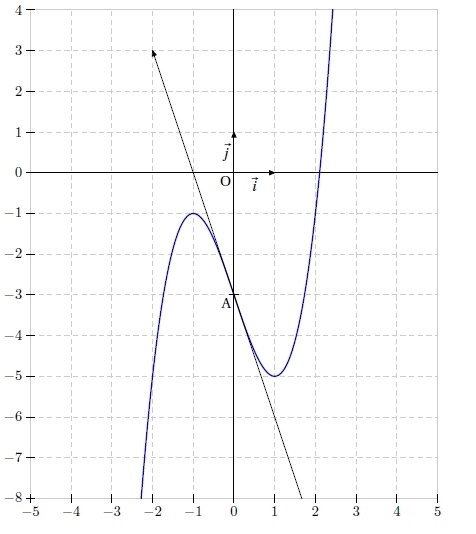
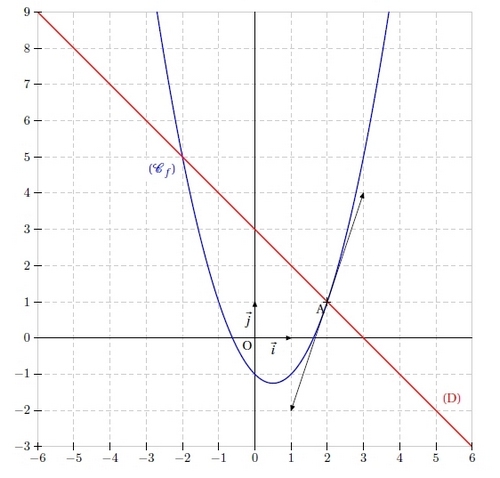
Exercice 11 – Etude de deux fonctions et des tangentes
On considère la fonction définie par .
On note (Cf ) sa courbe représentative.
On considère également la fonction g définie par g(x) = 3 – x.
On note (D) sa représentation graphique.
1. Calculer la dérivée f’ de f.
2. Déterminer une équation de la tangente (T) à la courbe (Cf ) au point d’abscisse .
3. Résoudre par le calcul l’équation g(x) = f(x).
4. Préciser les coordonnées des points d’intersections de (Cf ) et (D).
5. Tracer sur un même repère les droites (T), (D) et la courbe (Cf ).
Exercice 12 – Déterminer la dérivée de fonctions numériques
Dériver les fonctions suivantes :
Exercice 13 – Dérivée de plusieurs fonctions
Dériver les fonctions suivantes :
Exercice 14 – Valeur absolue et dérivabilité
Soit une fonction définie sur
par
.
Etudier la dérivabilité de sur
.
Exercice 15 – Dérivée d’une fonction puissance
Démontrez que si u est une fonction dérivable sur un intervalle I, alors:
a) u2 est dérivable sur I et (u2)’=2uu’.
b) u3 est dérivable sur I et (u3)’=3u2u’.
Exercice 16 – Sens de variation
On considère la fonction f définie par sur
.
1. Démontrer que pour tout x appartenant à
.
2. En déduire que la fonction f admet un maximum en .
3. Démontrer que .
4. En déduire que la fonction f est croissante sur l’intervalle et décroissante sur
.
Exercice 17
Soit la fonction définie sur
par
1. Etudier les variations de sur
.
2. Déterminer les coordonnées des points d’intersection entre la courbe représentative de et la droite
d’équation
.
Exercice 18
Etudier les variations sur de la fonction f définie par
.
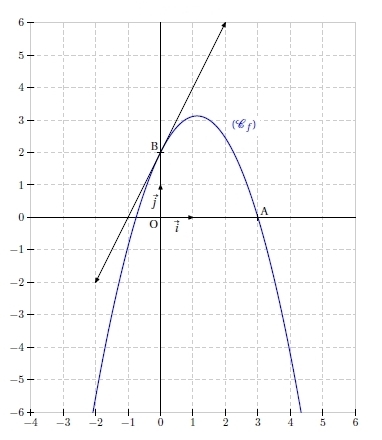
Exercice 19
Soit f la fonction définie sur par :
.
1. Etudier les variations de f sur .
2. Déterminer les coordonnées du point A, intersection entre la courbe représentative de f et l’axe des abscisses .
3. Déterminer une équation de la tangente T à la courbe représentative de au point A.
Exercice 20
Etudier les variations sur ]-2 ; 1[ de la fonction définie par :
.
Exercice 21 – Courbe représentative, dérivée et tangente
Soit la fonction définie sur
par
On appelle sa représentation graphique dans un repère orthonormal.
1) a) Etudier la parité de . Que peut-on en déduire pour
?
b) Déterminer l’expression de la fonction dérivée de et en déduire le tableau de variation de
2) a) Déterminer une équation de la tangente à au point d’abscisse 1.
b) Cette tangente recoupe en deux autres points.
b.1) Montrez que les abscisses de ces points sont les solutions de l’équation :
b.2) Vérifiez que l’on a :
b.3) En déduire les abscisses de ces points.
Exercice 22 – Parabole et tangentes
Soit (P) la parabole d’équation
et (H) l’hyperbole d’équation .
Le plan est ramené à un repère orthonormal.
1) Montrer que (P) et (H) rencontrent l’axe (Oy) en un même point A.
2) Montrer que les tangentes en A aux courbes (P) et (H) sont perpendiculaires.
Rappel : Dans un r.o.n deux droites sont perpendiculaires si et seulement si le produit de leur coefficient directeur est égal à –1 .
Exercice 23 – Tangente et déterminer un réel
Déterminer le réel m pour que la courbe d’équation
admette au point d’abscisse –1 une tangente de coefficient directeur 6.
Exercice 24 – Déterminer l’abscisse d’une tangente
Soit la fonction définie sur
et soit (C) sa courbe représentative.
Déterminer les abscisses des points de (C) où la tangente :
1) est horizontale
2) est parallèle à la droite d’équation .
Exercice 25 – Retrouver l’expression d’une fonction carrée
Une parabole admet dans un repère
une équation du type :
1. Déterminer les coefficients a, b et c sachant que coupe l’axe des abscisses au point A d’abscisse 3, l’axe des ordonnées au point B d’ordonnée 2 et qu’elle admet en ce point la droite d’équation y = 2x + 2 pour tangente.
2. Indiquer l’abscisse du second point d’intersection de avec (Ox).
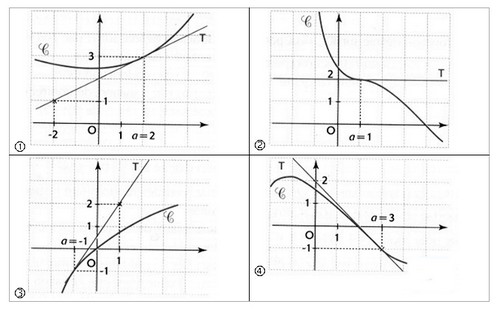
Exercice 26 – Nombre dérivée et tangente à une courbe
(C) représenter une fonction dérivable sur et la droite T est tangente à (C) au point d’abscisse a.
Dans chaque cas détermine et donner une équation de la tangente T.
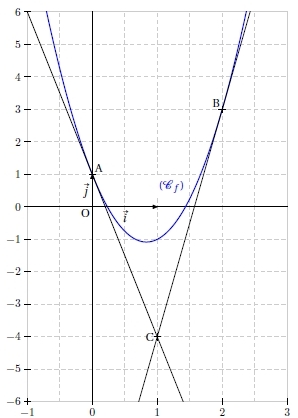
Exercice 27 – Equation de tangente à une parabole
On considère la fonction f définie par :
dont la parabole (Cf ) passe par les points A (0 ; 1) et B (2 ; 3).
Les tangentes en A et B se coupent au point C (1 ; – 4).
1. Déterminer une équation des tangentes à (Cf ).
En déduire f ‘ (0) et f ‘ (2).
2. Exprimer f ‘ (x) en fonction de a, b et c.
3. A l’aide des valeurs de f ‘ (0), f ‘ (2) et f(0), trouver trois équations vérifiées par a, b et c puis déterminer l’expression algébrique de la fonction f.
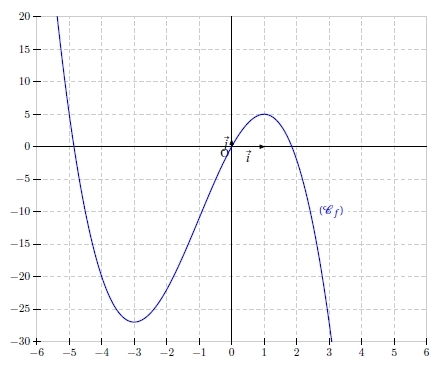
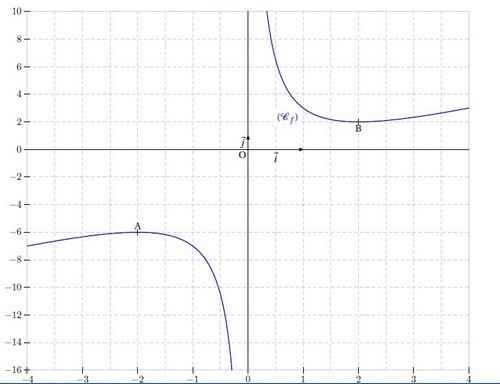
Exercice 28 – Limite en l’infini et tableau de variation
On considère la fonction définie sur
par
.
1. Calculer les limites de f en et en
.
2. Calculer la dérivée f » de f et étudier son signe.
3. Dresser le tableau de variation de la fonction f.
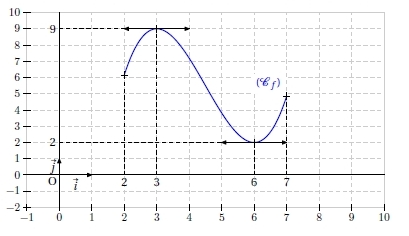
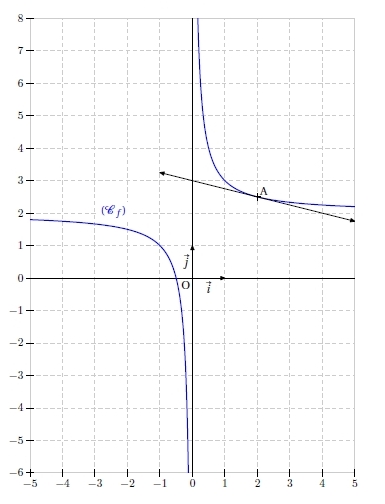
Exercice 29 – Lecture graphique
Ci-dessous est donnée la courbe (Cf ) représentant une fonction f définie et dérivable sur l’intervalle [2 ; 7].
1. Par lecture graphique, donner sans justifier la valeur de :
f(3) ; f ‘ (3) ; f(6) ; f ‘ (6).
2. Le graphique ne permet pas la lecture de f ‘ (4).
Préciser néanmoins son signe. Expliquer.
Exercice 30 – Calcul d’une dérivée et tableau de variation
Soit la fonction définie sur
par
.
1. Calculer la dérivée et étudier son signe.
2. Dresser le tableau de variations de la fonction f.
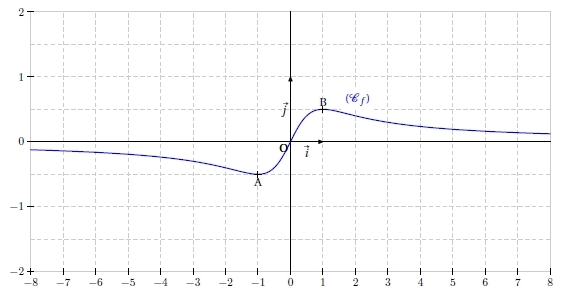
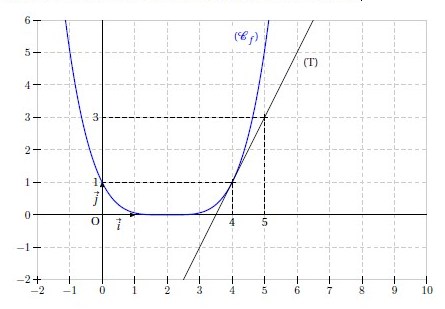
Exercice 31 – Lecture graphique du nombre dérivé
Sur le graphique ci-dessous sont représentées la courbe (Cf ) de la fonction f définie sur par :
ainsi que la tangente (T) à (Cf ) au point d’abscisse
.
1. Donner, par lecture graphique, et sans justifications, la valeur du nombre f ‘ (4).
2. Déterminer, à l’aide du calcul de la dérivée de f, la valeur du nombre f ‘ (3).
Exercice 32 – Dérivabilité en un point
Soit la fonction définie sur
par
.
1. Montrer que f est dérivable en 2.
2. Déterminer une équation de la tangente (T) à la courbe (Cf ) représentant f au point d’abscisse 2.
Exercice 33 – Calcul de dérivée et du nombre dérivé
1. Dériver les fonctions f et g définies ci-dessous :
2. Calculer f ‘ (16) et g ‘ (2).
Exercice 34 – Sens de variation et encadrement
1. Etudier le sens de variation de la fonction définie sur
par :
.
2. En déduire un encadrement de f(x) sur [0 ; 2].
Exercice 35 – Etude d’une fonction numérique
On considère la fonction définie sur
par
.
1. Calculer la dérivée f ‘ et étudier son signe.
2. Dresser le tableau de variations de la fonction f.
3. Tracer la représentation graphique (Cf ) de la fonction f sur.







 Mathovore c'est 13 926 848 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 926 848 cours et exercices de maths téléchargés en PDF.
Je veux les corrections