Sommaire de cette fiche
Les angles correspondants et alternes-internes avec un cours détaillé des différentes définitions et propriétés pour les élèves de cinquième (5ème).Ce chapitre et ces différentes propriétés nous permettront de démontrer que deux droites sont parallèles.
I. Angles et parallélisme
1.Vocabulaire
Définitions :
Dans la configuration ci-contre, deux droites (d) et (d’) sont coupées par une troisième droite.
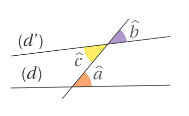
Les angles et sont opposés par le sommet.
Les angles et sont appelés angles correspondants.
Les angles et sont appelés angles alternes-internes.
2.Démontrer que deux droites sont parallèles
Propriété :
Si deux droites parallèles sont coupées par une troisième, alors elles forment :
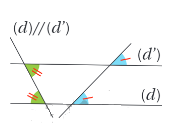
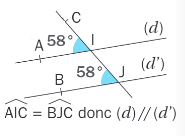
des angles correspondants de même mesure;
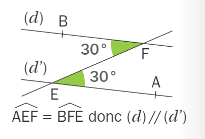
des angles alternes-internes de même mesure.
Propriété réciproque:
Si deux droites coupées par une troisième forment des angles correspondants de même mesure, alors ces droites sont parallèles.
Si deux droites coupées par une troisième forment des angles alternes-internes de même mesure, alors ces deux droites sont parallèles.
