Mis à jour le 23 avril 2025

cours maths 4ème

Théorème de Pythagore : cours de maths en 4ème en PDF.

Le théorème de Pythagore avec un cours de maths en 4ème faisant intervenir la partie directe et réciproque du théorème ainsi que la racine carrée d’un nombre positif et l’interprétation géométrique du théorème de Pythagore dans cette leçon en quatrième.

0-Introduction : un peu d’histoire….

Point de vue historique :
Pythagore de Samos, né vers -580 et mort vers -490, était un mathématicien, philosophe et astronome de la Grèce antique.

1. La racine carrée d’un nombre :

Définition :

Soit a un nombre positif.

On appelle racine carrée de a, notée \sqrt{a}, l’unique nombre positif dont le carré est égal à a.

C’est à dire : \,(\,\sqrt{a}\,\,)^2=a.

Exemple :

(\sqrt{16})=(\sqrt{4})^2=4

\sqrt{-9} n’a pas de sens car – 9 est un nombre négatif .

Application :

A l’aide de la calculatrice calculer  \sqrt{0},\sqrt{1},\sqrt{25},\sqrt{81},\sqrt{-5},\sqrt{49},\sqrt{0,36},\sqrt{104},\sqrt{7} .

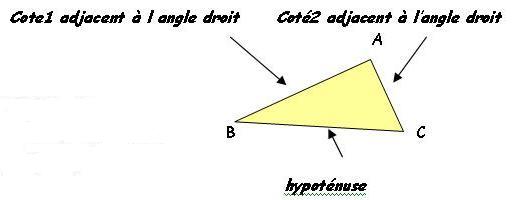
2- Le théorème de Pythagore:

2.1. Partie directe :

Côté adjacent et hypoténuse.

Théorème de la partie directe :

Si un triangle ABC est rectangle en A alors  BC²=AB²+AC².

(hypoténuse)²=(coté1)² + (coté2)²

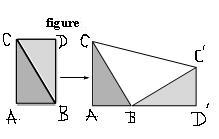
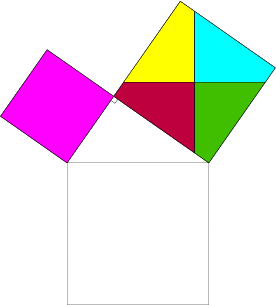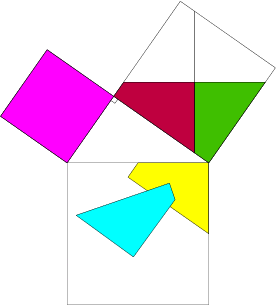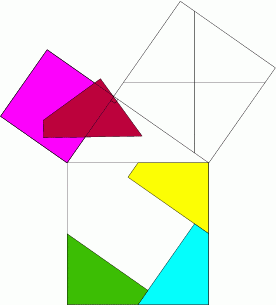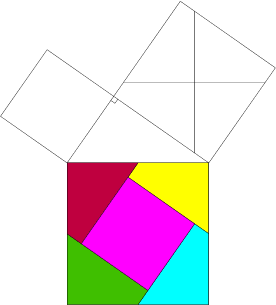
Preuve avec un trapèze :

Une des démonstrations de la partie directe du théorème de Pythagore.

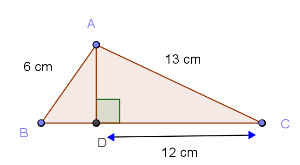
Soit un triangle ABC rectangle en A, montrons que BC^2\,=AB^2\,+\,AC^2.

Dans la figure ci-dessous, ABDC est rectangle de sens direct.

Théorème de Pythagore

On pose BC = a, AC = b et AB = c.

On considère le quart de tour de centre B (rotation de 90°)

qui transforme le triangle BCD en le triangle BC’D’.

Évidemment le triangle CBC’ est rectangle en B ‘car rotation de 90°).

Les points A, B et D’ sont alignés

et le quadrilatère AD’C’C est un trapèze.

En traduisant de deux manière l’aire de ce trapèze :

aire (AD’C’C) =aire (ABC) + aire (CBC’) + aire (BC’D’)

\frac{(b+c)^2}{2}=\frac{bc}{2}+\frac{a^2}{2}+\frac{bc}{2}

En multipliant par deux chaque membre de l’équation, nous obtenons :

(b+c)^2=a^2+2bc

(b+c)(b+c)=a^2+2bc (voir chapitre calcul littéral…)

b^2+bc+bc+c^2=a^2+2bc

b^2+2bc+c^2=a^2+2bc

En simplifiant par 2bc dans les deux membres,

Nous obtenons au final :

a^2\,=\,b^2\,+\,c^2

soit BC² = AC² + AB².

Remarque :

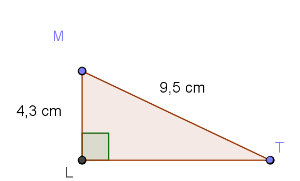
La partie directe du théorème de Pythagore, nous permet de déterminer une longueur du triangle connaissant les deux autres.

Signification géométrique :

BC^2=AB^2+AC^2

L’aire du carré de coté [BC] est égale à la somme des aires des carrés de coté [AB] et [AC]

Signification géométrique du théorème de Pythagore.

Théorème de Pythagore et aspect géométrique.

Théorème de Pythagore et une animation

2.2.- La réciproque du théorème de Pythagore.

Propriété de la partie réciproque :

Soit un triangle ABC tel que [BC] soit le côté le plus long.

Si BC^2=AB^2+AC^2 ALORS le triangle ABC est rectangle en A.

Propriété de la partie contraposée :

Soit un triangle ABC tel que BC est la plus grande longueur Si BC^2\neq\,AB^2+AC^2  ALORS le triangle ABC n’est rectangle.

Remarque :

La réciproque et la contraposée du théorème de Pythagore, nous permettent de déterminer si un triangle est rectangle connaissant les trois mesures de ses cotés.

Vous avez assimilé le cours sur le théorème de Pythagore en 4ème ?

Effectuez ce QCM de maths en quatrième sur le théorème de Pythagore afin d’évaluer vos acquis sur cette leçon.

Le théorème de Pythagore

QCM sur le théorème de Pythagore en quatrième.

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «théorème de Pythagore : cours de maths en 4ème en PDF.» au format PDF.

D'autres cours et exercices à consulter

Inscription gratuite à Mathovore.  Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

✕
Mathovore

GRATUIT
VOIR