Le parallélogramme : cours de maths en 5ème en PDF.

Sommaire

Le parallélogramme avec un cours de maths en 5ème où nous traiterons de la définition, des propriétés ainsi que des parallélogrammes particuliers comme le rectangle, le losange et le carré ainsi que la construction à la règle et compas en classe de cinquième au cycle 4.

I. Définition et vocabulaire :

1. Rappels :

Définition et vocabulaire

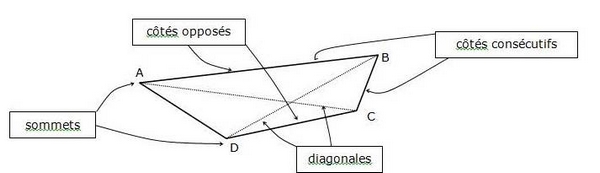
Un quadrilatère est une figure géométrique à 4 côtés.

Remarque :

Attention à l’ordre des lettres. Les quadrilatères ABCD et ABDC sont différents.

2. Le parallélogramme :

Définition

Un parallélogramme est un quadrilatère qui a ses côtés opposés deux à deux parallèles.

ABCD est un parallélogramme : (AB)//(DC) et (AD)//(BC)

II. Propriétés : lien avec la symétrie centrale .

Propriétés

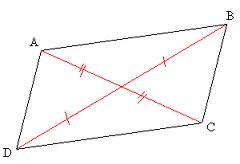
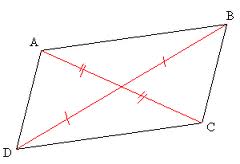
Dans un parallélogramme, le point d’intersection O des diagonales est le centre de symétrie du parallélogramme.

Remarque :

On dit alors que ABCD est un parallélogramme de centre O.

III. Conséquences

1. Les diagonales :

Propriété

Les diagonales d’un parallélogramme se coupent en leur milieu.

Démonstration :

O est le centre de symétrie donc par définition 0 est le milieu de [AC] et de [BD].

2. Les côtés :

Propriétés

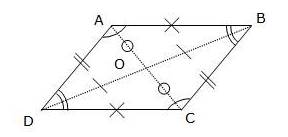
Les côtés opposés d’un parallélogramme sont de même longueur.

Démonstration :

Par symétrie par rapport à O, [AB] est l’image de [CD] et [AD] est l’image de [BC].

La symétrie centrale conserve les longueurs donc AB = CD et BC = AD.

3. Les angles :

Propriété

Les angles opposés d’un parallélogramme sont égaux deux à deux.

Démonstration :

La symétrie centrale conserve les angles et comme un parallélogramme a pour centre de symétrie le point d’intersection de ses diagonales alors les angles opposés d’un parallélogramme sont de même mesure.

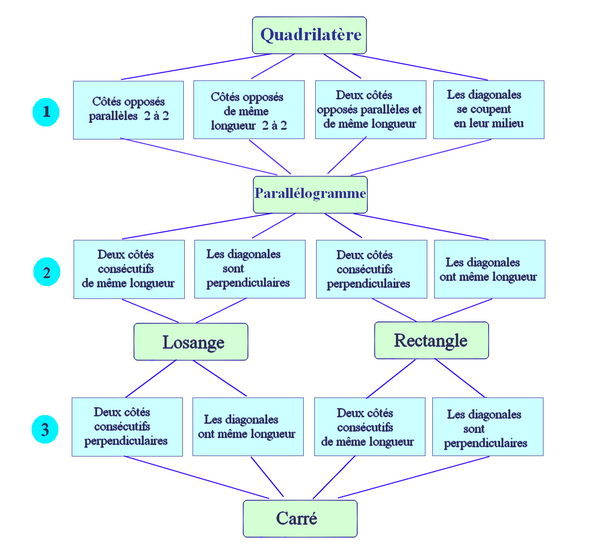
IV. Les parallélogrammes particuliers :

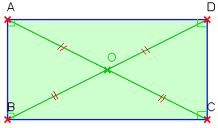
1.Le rectangle

Propriété

Si un parallélogramme a un angle droit alors c’est un rectangle.
Si un parallélogramme a ses diagonales de même longueur alors c’est un rectangle.

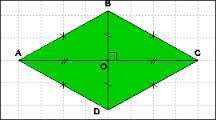
2.Le losange

Propriétés

Si un parallélogramme a ses diagonales perpendiculaires alors c’est un losange.
Si un parallélogramme possède deux côtés consécutifs égaux alors c’est un losange.

Remarque :
Le losange possède deux axes de symétrie : ses diagonales.

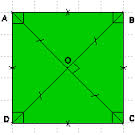
3.Le carré

Propriété

Si un parallélogramme est à la fois un rectangle et un losange alors c’est un carré.

V.Bilan sur le parallélogramme :

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «le parallélogramme : cours de maths en 5ème en PDF.» au format PDF.

D'autres cours et exercices à consulter

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.