Exercice 1
Soit la fonction linéaire .
a. Calculer f(5) ; f(- 1,2) ; f(0) ; f(100).
b. Calculer les nombres x dont les images sont 2 400 ; – 45.
Exercice 2
Soit g la fonction linéaire telle que .
a. Quel est le coefficient de la fonction g ?
b. Calculer les images de 10 ; – 5 et 1.
c. Compléter les égalités suivantes :
g (10)= … g (- 5 ) = … et g(……)= – 0,4.
Exercice 3
On sait que 18 a pour image 23 par la fonction f et que 12 a pour image 14 par f.
f est-elle une fonction linéaire ?Pourquoi ?
Exercice 4
Exprimer la fonction linéaire f sous la forme ( le nombre a est à déterminer), puis calculer f(0) ; f(1) et f( – 2).
1. Lorsque l’image de 10 est – 3.
2. Lorsque f (- 100)= – 46.
3. Lorsque le coefficient de f est 2,5.
Exercice 5
Dans un repère,
a. Tracer la droite d représentant la fonction .
b. Tracer la droite d d’équation y = 1,2x.
Quelle fonction la droite d représente-t-elle ?
c. Tracer la droite d’ représentant la fonction linéaire g de coefficient a = – 2.
Exercice 6
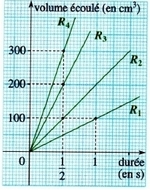
Sur le graphique ci-dessous sont représentées des fonctions linéaires qui donnent la quantité d’eau débitée par quatre robinets en fonction de la durée de l’écoulement.
Retrouver le débit moyen de chaque robinet
On exprimera les résultats en puis en
.
Exercice 7
Représenter graphiquement les fonctions linéaires suivantes sur un même repère orthonormé (même graphique sur les deux axes perpendiculaires).
Exercice 8
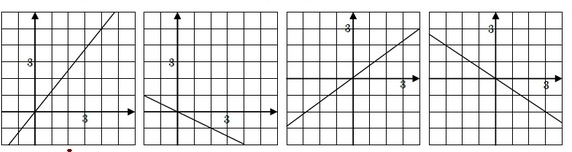
Calculer les coefficients des fonctions linéaires représentées ci-dessous.
Exercice 9
Un avion se déplace à une vitesse constante de 900 km/h.
f est la fonction qui, à la durée du déplacement en heure associe la distance parcourue en km.
a. Dans un repère (unités graphiques : 1 cm pour une heure en abscisse et 1 cm pour 500 km en ordonnée), tracer la demi-droite qui représente cette fonction f.
b. Lire f(10) sur le graphique et vérifié votre résultat par le calcul.
Exercice 10 – Courbes et représentation graphique
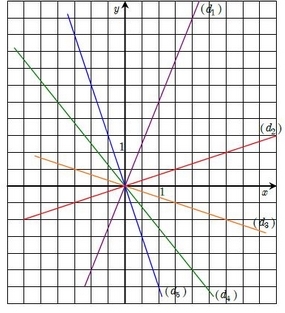
On considère le repère du plan ci-dessous, dans lequel on a tracé les droites
A partir de ce graphique, retrouver dans la liste ci-dessous les équations des droites
Exercice 11 :
On considère f et g deux fonctions linéaires.
Le coefficient de f est – 3 et on sait que g(3)=6.
a. Calculer l’image de 2 et l’image de – 4 par la fonction f.
b. Déterminer le coefficient de l’application linéaire g.
c. Représenter graphiquement f et g dans un repère orthonormal.
Exercice 12 :
On dispose dune citerne que l’on rempli d’eau.
On note le volume d’eau et la durée de remplissage.
| Temps en minutes | 10 | 15 | 50 |
| Volime en litres | 400 | 600 | 2 000 |
a. La durée de remplissage et le volume d’eau sont-ils proportionnels ?
b. On appelle x le volume en litres, montrer que la durée de remplissage est une fonction linéaire de x.
c. Représenter graphiquement cette fonction pour tout x compris entre 0 et 3 000.
d. Utiliser ce graphique pour déterminer une valeur approchée :
– de la durée de remplissage pour un volume de 1 300 litres.
– du volume obtenu au bout de 26 minutes.
e. Retrouver le résultat par le calcul.
Exercice 13 :
La population d’une ville augmente de 2 % par an.Soit x cette population.
Montrer que la population de l’année suivante est une fonction linéaire que l’on précisera.
Si cette population est de 100 000 habitants, quelle sera la population au bout de 5 ans ?
Exercice 14 – Déterminer une fonction linéaire
f est une fonction linéaire .
Déterminer l’expression de f(x) en sachant que
Exercice 15 – Pourcentages d’augmentation et baisse
a) Soit : x le prix initial d’un article et : y son prix final après une augmentation ou une baisse. Quel est le pourcentage d’augmentation ou de baisse dans chacun des cas suivants ?
(1): y = 1.4x
(2): y = 0.5x
(3): y = 0.9x
(4): y = 1.05x
Exercice 16 – Pourcentages , augmentation et réductions
1. Un objet A coûte 65 euros. Son prix augmente de 5%.
Combien coûte-t-il après cette augmentation?
2.Un objet B coûte 88 euros après une augmentation de 10%.
Quel était son prix avant cette augmentation?
3.Un objet C coûte 45 euros. Après une augmentation son prix est de 50,40 euros.
Quel est le pourcentage de cette augmentation?
Exercice 17 – Gérant de magasin de vêtements
Un gérant de magasin de vêtements décide de baisser ses prix de 15 % .
a) Quelle est la fonction linéaire modélisant cette baisse ?
b) Quelle est le nouveau prix d’un pantalon qui coûtait 70 e avant cette baisse ?
c) Quel est l’ancien prix d’un pull qui coûte 50,12 € après cette baisse ?
Exercice 18 – Calcul d’images
On considère la fonction linéaire f de coefficient – 5.
Calculer l’image par f des nombres suivants :
a) 0
b) 3
c) – 2
d)
e)
Exercice 19 – Quelles sont les fonctions linéaires ?
Pour chaque fonction, préciser si elle est linéaire et, dans ce cas, son coefficient.
a)
b)
c)
d)
e)
f)
Exercice 20 – Volume d’un parallélépipède
L’unité est le centimètre.ABCDFEGH et BIJCELKG sont deux pavés droits.
a. Exprimer les volumes du pavé bleu et
du pavé vert en fonction de x.
b. Dans un tableur, construire un tableau de valeurs et les courbes représentatives de et
en fonction de x.
c. Quel(s) nombre(s) a (ont) la même image par et
?
Exercice 21 – Images et antécédents
Soit f la fonction linéaire définie par : .
1.Calculer f(3), f(-2), f(7).
2.Quelles sont les images par f de -1, 6, ?
3.Trouver le nombre qui a pour image 7.





 Mathovore c'est 13 931 215 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 931 215 cours et exercices de maths téléchargés en PDF.
Une série d’exercice bien choisie et permet aux élèves de bien assimiler les premières notion de la fonction linéaire .
Merci beaucoup pour votre effort
Merci pour votre commentaire, nous sommes heureux de savoir que notre site vous serve.