Exercice 1 :
Ecrire sans parenthèses les expressions données :
a. -(3+x)
b. -(2a+4)
c. -(-3+x)
d. -(5-x)
e. -(7-2y)
f. -(-6-4x)
Exercice 2 :
Réduire chacune des expressions suivantes :
a.
b.
c.
d.
e.
f.
g.
h.
i.
j.
Exercice 3 :
Supprimer les parenthèses puis réduire chaque expression.
a.
b.
c.
d.
e.
f.
g.
Exercice 4 :
Développer puis réduire les expressions.
a.
b.
c.
d.
e.
f.
Exercice 5 :
Développer puis réduire les expressions.
a.
b.
c.
d.
e.
f.
g.
Exercice 6 :
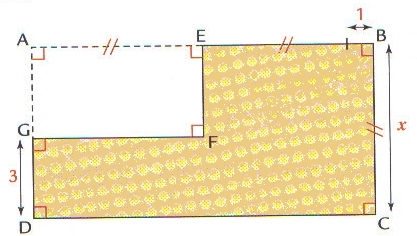
Dans cet exercice désigne un nombre supérieur à 3.
On se propose d’exprimer l’aire de la surface coloriée en fonction de
1.a. Expliquer pourquoi l’aire :
• du rectangle ABCD peut s’écrire ;
• du rectangle AEFG peut s’écrire .
b. Après avoir développé les expressions littérales précédentes, exprimer l’aire en fonction de
.
• Montrer que l’aire peut s’écrire aussi :
.
• Développer puis réduire cette expression.
3.Calculer alors la valeur de pour
.
Exercice 7 :développement d’expressions algébriques
A = x (x + 2)
B = 5x (x +3)
C = 2x (3x – 5)
D = – 3x (1 – 4x)
E = (x + 2) (-x + 3)
F = (2x + 3) (4x – 1)
G = (5 – 3y) (6 – 2y)
Exercice 8 : Développer et réduire.
A = (x + 3) (x – 2) + (2x + 4) (x + 5)
B = (2x – 1) ( 7x + 8) – (5 – 4x) (3x + 1)
C = (3x + 4) ( 7x – 1) – (2x + 5) (3x – 2)
Exercice 9 :
A = (x – 3) (3x – 1) – 2x² + 4
Calculer A pour : x = 2 x = -1
Exercice 10 :
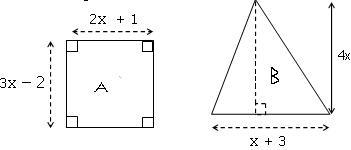
Exprimer sous forme développée et réduite l’aire de ces deux figures.
Exercice 11 :
Factoriser en recherchant un facteur commun.
A = 11n + 11
B = x ² + 5x
C = 14t² – 21t
D = (x + 5)(x + 8 ) + 2 (x + 5)
E = (2x – 9) (3x + 7) + (2x – 9) (6 – 2x)
F = (5x – 3) (7x – 9) – (3x + 4) (5x – 3)
G = (7x + 1) ² + (7x + 1) (2x + 5)
H = (2a +3) (5a – 1) – (2a +3)²
Exercice 12 -Activité d’introduction au calcul littéral
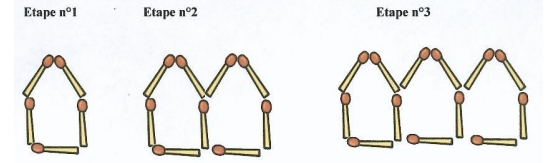
On représente par étape des maisons à l’aide d’allumettes comme cela est fait ci-dessous.
1. Combien faudra-t-il d’allumettes aux étapes n°4 et n°10 ? Répondre sans faire de dessin.
2. Vérifier si vous aviez trouvé le bon nombre
3. Combien d’allumettes faudra-t-il à l’étape n° 2007 ?
4. Comment exprimer le nombre d’allumettes pour une étape quelconque ?
Exercice 13 -Introduction au calcul littéral
Le professeur a écrit au tableau l’exercice suivant :
Calculer
23 × 7 + 3 ;
23 × 8 + 3;
23 × 9 + 3;
23 × 10 + 3
23 × 11 + 3;
23 × 12 + 3;
23 × 13 + 3;
23 × 14 + 3
Un camarade est absent.
Quelle consigne lui donner au téléphone, sans lui dicter tous les calculs.
La consigne est bonne si le camarade sait exactement ce qu’il doit faire.
Exercice 14 -Calcul d’une vitesse moyenne
1) Un randonneur parcourt 5 km en 1 heure et 15 minutes. Quelle est sa vitesse moyenne en km/h ?
Justifier
2) Une voiture roule à la vitesse de 50 km/h. En combien de temps parcourt-elle 110 kilomètres ? Donner
le résultat en heures et minutes.
Exercice 15 -Donner l’expression littérale
a désigne un nombre décimal non nul .
Donner une expression littérale de :
1) le double du carré de a .
2) le carré du double de a .
3) la moitié du carré de a :
4) le carré de la moitié de a .
5) le carré de l’opposé de a .
6) l’opposé du carré de a .
7) le carré de l’inverse de a .
8) l’inverse du carré de a .
Exercice 16 -Appliquer les propriétés et règles de calcul
1. Simplifier les écritures suivantes :
2. développer et réduire les expressions suivantes :
Exercice 17 -Salle de concert
Une salle de concert peut contenir 600 places. Il y a x places assises et les autres sont debout. Les places debout coûtent 15€ et les places assises 25€.
1°) Que représentent les expressions : a- 600 – x ? b- 25x ? c- 15 (600 – x) ?
2°) Exprime, en fonction de x la recette totale en euros si toutes les places sont occupées.
3°) Calcule cette recette si x = 200.
4°) Quel est le nombre de places assises si la salle est comble et si la recette est de 12 500 € ?
Exercice 18 -Développer les expressions suivantes
A = 6 (2x + 8) B = 7 (5x − 1) C = -4x (x − 9)
D = (3x + 4) (2x + 3) E = (7x + 5) (5x + (-3)) F = (2x + 9) (7x − 1)
Exercice 19 -Programme de calcul
On donne un programme de calcul :
Choisir un nombre.
Lui ajouter 2
Multiplier la somme obtenue par le nombre choisi
Ajouter 1 à ce produit
Ecrire le résultat.
1) Ecrire les calculs permettant de vérifier que si l’on fait fonctionner ce programme avec le nombre – 1 , on obtient 0.
2) Donner le résultat fourni par le programme lorsque le nombre choisi est -6
3) Donner le résultat fourni par le programme lorsque le nombre choisi est 4
4) Ecrire l’expression obtenue pour un nombre a quelconque.
Exercice 20 -Développer et réduire
a) Supprimer les parenthèses puis réduire l’expression M
b) Développer et réduire N et P.
c) Calculer N lorsque x est égal à 3.
Exercice 21 -Programme de calcul de mr Hamraoui
Mr Hamraoui demande a Anna de suivre les instructions suivantes:
– Choisis un nombre ;
– Multiplie le par -11 ;
– Ajoute 8 ;
– Multiplie le résultat par -9 ;
– Ajoute le nombre choisi au départ ;
– Ajoute -28 ;
– Donne ton résultat .
Anna: Je trouve 400 .
M. Hamraoui : Tu avais donc choisi 5 au départ .
Quel est le truc de Mr Hamraoui ?
Exercice 22 -Introduction au calcul littéral et géométrie
Une piscine rectangulaire mesure 10 m sur 5 m.
On désire aménager tout autour une plage.
Cependant cette plage ne doit pas avoir une superficie trop importante pour ne pas coûter trop cher à la collectivité, mais ne doit pas être trop petite pour ne pas pénaliser les non baigneurs.
On estime que la superficie de la plage doit être comprise entre 110 et 120 .
On décide alors de faire un avant-projet de piscine, en notant le nombre désignant la largeur de la plage.
Le nombre devient alors ce que l’on appelle une inconnue .
1. Calculer l’aire de cette plage dans le cas où , puis dans le cas où
, et enfin
2. Dans chacun des cas précédents, peut-on lancer le projet de construction ? Pourquoi ?
3. Quelle méthode pouvez-vous proposer pour trouver une largeur de plage satisfaisante ?
Pour accélérer la recherche de cette largeur idéale, on essaie d’exprimer en fonction du nombre , l’aire de cette plage.
Deux équipes vont y travailler :
– Calculer l’aire du rectangle ABCD, à laquelle on retranche l’aire de la piscine.
– Assembler les éléments de la plage comme indiqué sur le croquis ci-dessous.
4. Retrouver les expressions obtenues par chacune des deux équipes.
5. Proposer une largeur possible de plage pour lancer le projet.
Exercice 23 -Développer et réduire les expressions suivantes :
Exercice 24 -Calculs contenant des parenthèses
Supprimer les parenthèses puis réduire les expressions :
Exercice 25 -Identités remarquables
En se rappelant que .
développer et réduire les expressions suivantes :
Exercice 26 -Calcul algébrique
Réduire chaque expression littérale suivante :
Exercice 27 :
Réduire chacune de ces expressions :
Exercice 28 :
1. Développer et réduire les expressions suivantes.
2. Tester le résultat pour x = 0 et x = 1.
a.
b.
Exercice 29 -Programme de calcul
Voici un programme de calcul :
– Choisir un nombre.
– Soustraire 3 à ce nombre.
– Multiplier le résultat obtenu par – 5 .
– Diviser le résultat obtenu par 4.
– Ajouter le nombre de départ au résultat obtenu.
1. Effectuer ce programme de calcul pour – 2 et pour 7.
2. Reprendre ce programme pour un nombre x.
Exercice 30 -Du texte à l’écriture mathématique
Écrire le plus simplement possible en fonction de x :
a. «le double de x augmenté de 1 » ;
b. «la somme de 3 et du triple de x » ;
c. «le tiers de x, diminué de 5 » ;
d. « le produit par 5 de la somme de x et de 4 » ;
e. «la somme de 6 et du produit de x par 7».
Développer et réduire les expressions suivantes :
Exercice 31 -Réduire des expressions algébriques
Réduire chacune des expressions suivantes :
Exercice 32 -Suppression de parenthèses
Supprimer les parenthèses puis réduire les expressions suivantes :
Exercice 33 -Réduction d’expressions littérales
Réduire, si possible, les expressions suivantes :









 Mathovore c'est 13 927 330 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 927 330 cours et exercices de maths téléchargés en PDF.