Produit scalaire : exercices de maths en terminale corrigés.

exercices de maths en terminale S

Des exercices de maths en terminale sur le produit scalaire, vous pouvez également travailler avec les exercices corrigés en terminale en PDF ou consulter la liste ci-dessous avec les corrections détaillées.

Exercice 1 – Calculer la distance d’un point à un plan

Calculer la distance du point M(5; 2; −3) au plan d’équation x + 4y + 8z = −2.

Exercice 2 – Un plan formé par trois points

Soient A(1; −1; 1), B(0; 2; −1) et C(−1; 1; 0).

Montrer que A, B et C forment un plan puis déterminer x aﬁn que $\vec{u}$ (x; 3; 4) soit normal à (ABC).
Exercice 3 – Plans orthogonaux

Les plans P : 2x − y + z + 9 = 0 et Q : x + y − z − 7 = 0 sont-ils orthogonaux ?

Exercice 4 – Equation cartésienne d’un plan

Déterminer une équation cartésienne du plan P passant par A(−2; 1; 3) et orthogonal
à (BC) où B(1; −2; 2) et C(4; 1; −1).

Exercice 5 – Déterminer l’équation cartésienne d’un plan

Déterminer une équation cartésienne du plan contenant A(2; −1; 1) et orthogonal au

vecteur $\vec{n}$ (3; −4; 2).

Exercice 6 – Vecteur normal et plan

Le vecteur $\vec{n}$ (6; −2; 4) est-il normal au plan d’équation −3x + y − 3z = 1 ?

Exercice 7 – Vecteur normal d’un plan

Déterminer un vecteur normal au plan d’équation 31x + 37y + 41z + 43 = 0.

Exercice 8 – Calcul de la mesure d’un angle
On se place dans un repère orthonormal.

Soient A(−1; 1; 2), B(0; 1; 0) et C(2; 0; 3).

Calculer une mesure approchée de l’angle $\widehat{BAC}.$ .

Exercice 9 – Produit scalaire et cube

Soit ABCDEFGH un cube d’arête a.

Calculer :

$1.\,\vec{AE}.\vec{AF}.\\2.\,\vec{AE}.\vec{AG}.\\3.\,\vec{AF}.\vec{HC}.$

Exercice 10 – Tétraèdre régulier

Soit ABCD un tétraèdre régulier d’arête a.

Calculer $\vec{AB}.\vec{AC}.$

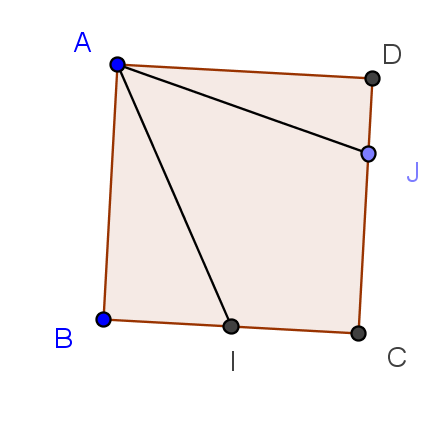
Exercice 11 – Etudier un carré

ABCD est un carré de coté 8 unités.

Les points I et J sont définis pas $\vec{BI}=\frac{1}{2}\vec{BC}$ et $\vec{DJ}=\frac{1}{3}\vec{DC}$ .
1. Exprimer le produit scalaire $\vec{AI}.\vec{AJ}$ de deux façons différentes .

2. Déterminer $cos(\widehat{IAJ})$ , puis la mesure de cet angle en radians .

Exercice 12 – Ensemble de points

ABC est un triangle équilatérale de côté de longueur .

Quel est l’ensemble des point M tels que :

$(\vec{MA}+2\vec{MB}+\vec{MC}).(\vec{MA}-2\vec{MB}+\vec{MC})=2l^2$

Cette publication est également disponible en : English (Anglais) Español (Espagnol) العربية (Arabe)

Télécharger et imprimer ce document en PDF gratuitement

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «produit scalaire : exercices de maths en terminale corrigés en PDF.» au format PDF.

D'autres fiches dans la section exercices de maths en terminale S

Télécharger nos applications gratuites avec tous les cours et exercices corrigés.

D'autres fiches similaires à produit scalaire : exercices de maths en terminale corrigés en PDF..

Calcul littéral : exercices de maths en 3ème corrigés en PDF.
63
Des exercices sur le calcul littéral en 3ème et les identités remarquables , vous pouvez également vous entraîner en consultant une année d'exercices sur le calcul littéral au format PDF en troisième. Exercice 1 - Développer avec les identités remarquables. Développer en utilisant les identités remarquables : Exercice 2 - Développer une expression…
Calcul littéral : exercices de maths en 4ème corrigés en PDF
63
Des exercices de maths en quatrième (4ème) sur le calcul littéral dont la simple distributivité et double distributivité. Exercice 1 : Ecrire sans parenthèses les expressions données : a. -(3+x) b. -(2a+4) c. -(-3+x) d. -(5-x) e. -(7-2y) f. -(-6-4x) Exercice 2 : Réduire chacune des expressions suivantes : a.…
Priorités et calculs : exercices de maths en 5ème corrigés en PDF.
62
Des exercices sur les opérations et priorités opératoires en cinquième pour s'exercer en 5ème.Ces fiches sont à imprimer en PDF. Exercice 1 - Calculer les expressions. Calculer les expressions suivantes en écrivant les étapes intermédiaires : a) b) …

Les dernières fiches mises à jour.

Voici les dernières ressources similaires à produit scalaire : exercices de maths en terminale corrigés en PDF. mis à jour sur Mathovore (des cours, exercices, des contrôles et autres), rédigées par notre équipe d'enseignants.

Mathovore c'est 13 703 363 cours et exercices de maths téléchargés en PDF.