Géométrie dans l'espace : exercices de maths en 1ère corrigés.

exercices de maths en 1ère S

Des exercices de maths en 1ère sur la géométrie dans l’espace.

Exercice 1 – Cercle et lieux de points
Il est vivement recommandé d’utiliser un logiciel de géométrie…

1. Partie préliminaire :
on considère un triangle ABC, G son centre de gravité,
Ω le centre de son cercle circonscrit et H son orthocentre.

Montrer que H est l’image de Ω dans une homothétie de centre G dont on précisera le rapport.

2. On considère un cercle Γ de centre O, de rayon R, passant par un point fixe A.
Soient B et C deux points de Γ tels que la distance BC soit constante et égale à l.

a. Quel est le lieu géométrique des milieux I de [BC] ?

b. Quel est le lieu géométrique des centres de gravité G de ABC ?

c. Quel est le lieu géométrique des orthocentres H de ABC ?

3. Reprendre la partie 2. avec BC sur une droite ∆ ne passant pas par A, A fixe.

Exercice 2 – Homothéties et droites parallèles
ABC est un triangle isocèle (AB = AC).
E et F sont deux points du segment [BC].
Les parallèles à (AB) menées par E et F coupent (AC) en G et H respectivement.
Les parallèles à (AC) menées par E et F coupent (AB) en I et J respectivement.

1. Montrer que GH = IJ.

2. Quelle condition doivent vérifier E et F pour que (JG) et (IH) soient parallèles ?

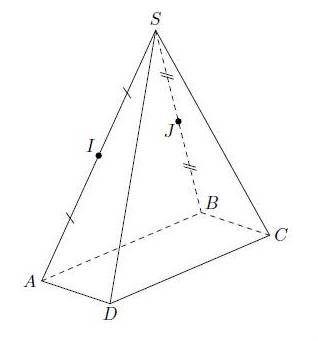
Exercice 3 – Pyramide à base triangulaire
La pyramide SABCD est à base rectangulaire.

On appelle I le milieu de [SA] et J le milieu de [SB].

Déterminer l’intersection des plans (DIJ) et (SAC).

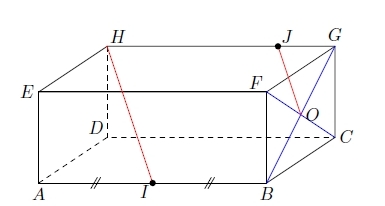
Exercice 4 – Etude d’un pavé droit
ABCDEFGH est un pavé droit.
On note I le milieu de l’arête [AB] et J le point tel que $\vec{HJ}=\frac{3}{4}\vec{AB}$ .

O est le centre de la face BCGF.

Démontrer que les droites (IH) et (JO) sont parallèles.

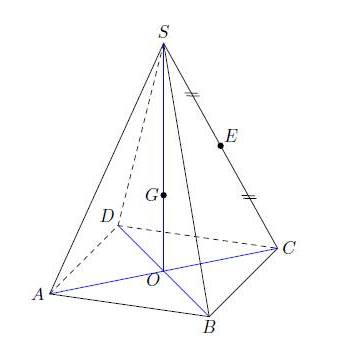
Exercice 5 – Etude d’une pyramide
SABCD est une pyramide à base carrée ABCD de centre O.

G est le centre de gravité du triangle SBD et E est le milieu du segment [SC].

Démontrer que les points A, G et E sont alignés.

Exercice 6 – Points coplanaires
L’espace est rapporté à un repère orthonormal direct $(O;\vec{i},\vec{j},\vec{k})$ .

On considère les points :

A(1 ; 0 ; – 1) B( – 1 ; 0 ; 0) C(1 ; – 6 ; 4) D(4 ; – 9 ; 5) E(3 ; – 6 ; 3)

1. Montrer que les points A, B, C et D sont coplanaires.

2. Montrer que le point D appartient à la droite (AE).

3. Montrer que ABCE est un parallélogramme. Est-ce un rectangle ? Est-ce un carré ?

Exercice 7 – Points alignés
On donne A (1 ; – 2 ; 3), B (0 ; 4 ; 4) et C (4 ; – 20 ; 9).

Les points A, B et C sont-ils alignés ?

Exercice 8 – Nature d’un triangle
On donne A(1 ; 1 ; 3), $B(\sqrt{2}+1;0;2)\,et\,C(\sqrt{2}+1;2;2).$

Quelle est la nature du triangle ABC ?

Exercice 9 – Droites parallèles
On donne A( – 3 ; 1 ; 4), B( – 2 ; – 1 ; 7), C( – 4 ; – 1 ; – 2) et D(- 5 ;- 5 ; 4).

Les droites (AB) et (CD) sont-elles parallèles ?

Exercice 10 – Calculer les coordonnées d’un barycentre
On donne A(2 ; – 1 ; 3), B(1 ; 2 ; 0), C( – 2 ; 1 ; 2) et D( -1 ; – 2 ; 5).

1. ABCD est-il un parallélogramme ? Un rectangle ?

2. Calculer les coordonnées de l’isobarycentre du quadrilatère ABCD.

Cette publication est également disponible en : English (Anglais) Español (Espagnol) العربية (Arabe)

Télécharger et imprimer ce document en PDF gratuitement

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «géométrie dans l'espace : exercices de maths en 1ère corrigés en PDF.» au format PDF.

D'autres fiches dans la section exercices de maths en 1ère S

Télécharger nos applications gratuites avec tous les cours et exercices corrigés.

D'autres fiches similaires à géométrie dans l'espace : exercices de maths en 1ère corrigés en PDF..

Barycentre : exercices de maths en 1ère corrigés en PDF.
66
Des exercices sur le barycentre en 1ère avec l'utilisation de la définition du barycentre de n points pondérés et des propriétés du barycentre comme l'associativité. Tous ces exercices en première disposent d'un corrigé détaillé afin que les élèves puissent réviser en ligne. Exercice 1 - Barycentre de points pondérés 1.…
Nombres complexes : exercices de maths en terminale corrigés en PDF.
64
Des exercices sur les nombres complexes en terminale faisant intervenir la notion de conjugué, d'argument, les formules de Moivre et d'Euler ainsi que les écritures arithmétiques et géométriques. Exercice 1 : Mettre les nombres complexes sous la forme a + ib (a et b réels). Exercice 2 : Soit z=x+iy…
Vecteurs et translation : exercices de maths en 2de corrigés en PDF.
63
Des exercices de maths sur les vecteurs et la translation en classe de 2de. Vous trouverez pour chaque exercice sa correction détaillée en seconde. Exercice 1 - Les point sont-ils alignés Les points P, Q et R sont-ils alignés ? Exercice 2 - Points alignés et vecteurs ABCD est un…

Les dernières fiches mises à jour.

Voici les dernières ressources similaires à géométrie dans l'espace : exercices de maths en 1ère corrigés en PDF. mis à jour sur Mathovore (des cours, exercices, des contrôles et autres), rédigées par notre équipe d'enseignants.

Mathovore c'est 13 624 707 cours et exercices de maths téléchargés en PDF.