Sommaire de cette fiche
0. Point de vue historique :
Le mot « vecteur » vient du latin « vehere » (conduire, transporter)La notion de vecteur est le fruit d‘une longue histoire, commencée voici plus de deux mille ans.
I. Les vecteurs :
1.Définition et vocabulaire :
Un vecteur est un objet mathématique défini par :
– une direction;
– un sens;
– une longueur.
On le représente par une flèche .
Si on représente cette flèche à partir d‘un point A (appelée origine) et qu‘on note B son extrémité,
alors :
– La direction du vecteur est celle de la droite (AB),
– Le sens du vecteur est le sens de l‘origine A vers l‘extrémité B,
– La longueur (appelée norme) du vecteur est la longueur AB du segment [AB].
On a :
– Le vecteur est l‘opposé du vecteur
.
On a
– est appelé le vecteur nul et est noté
.
2. Egalité de deux vecteurs :
– a. Deux vecteurs et
sont égaux si et seulement si :
Les vecteurs et
ont même direction, le même sens et la même longueur (norme).
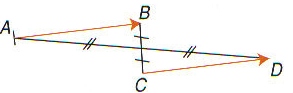
– b. La translation qui transforme A en B transforme aussi C en D;
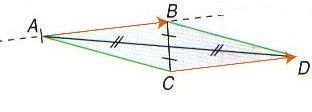
– c. Le quadrilatère ABDC, est un parallélogramme.(éventuellement aplati) ;
Réciproquement,
si ABDC est un parallélogramme alors
3. Milieu d‘un segment :
Soint A et B deux points distincts du plan .
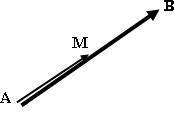
– Si M est le milieu de [AB], alors .
– Réciproquement, si
alors M est le milieu de [AB].
II. La translation :
1. Vocabulaire :
– Lorsque deux droites sont parallèles, on dit qu‘elles ont la même direction- Il y a deux sens de parcours sur une droite : de A vers B ou bien de B vers A
– dans la direction de la droite (AB)
– dans le sens A vers B, que l‘on indique par la flèche
– d‘une longueur égale à AB.
On dit que le dessin en position B est l‘image du dessin en position A par la translation qui transforme A en B
ou, autrement dit,
par la translation de vecteur .
2. Propriétés des translations :
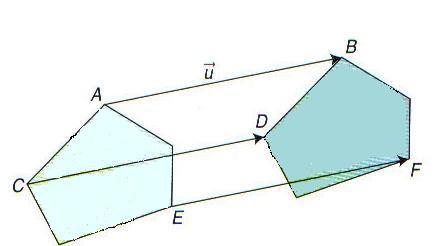
Construire l‘image d‘une figure par une translation revient à faire glisser cette figure dans une direction, un sens et avec une longueur donnée.
Un tel glissement n‘entraîne pas de déformation ni de changement de disposition .
Dans une translation ;
– les longueurs;
– le parallélisme;
– la perpendicularité;
– les angles
sont conservés.
– Une translation transforme une droite en une droite parallèle.
– Par une translation, une figure géométrique est transformée en une figure géométrique semblable.
– Pour construire l‘image d‘une figure géométrique, on ne construit donc que l‘image de ses points caractéristiques :
– pour un segment, ses extrémités;
– pour un triangle, ses trois sommets;
– pour un cercle, son centre et son rayon.
3. Egalité de deux vecteurs :
– a. La translation qui transforme A en B transforme aussi C en D;- b. Le quadrilatère ABDC, est un parallélogramme.(éventuellement aplati) ;
III. Composée de deux translations et somme de deux vecteurs :
Soient A, B et C trois points du plan, la composée de la translation de vecteur suivie de la translation de vecteur
est la translation de vecteur
.
On dit que le vecteur est la somme des vecteurs
et
.
On note :
( cette relation est appelée « relation de Chasles »)
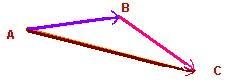
On utilise la méthode du << bout à bout>>,
C‘est à dire qu‘on représente le vecteur et a son extrémité on ajoute le vecteur
et on obtient le vecteur
qui est égal au vecteur
(d‘après la relation de Chasles).
L‘extrémité de l‘un est aussi l‘origine de l‘autre .
IV. Composée de deux symétrie centrales :
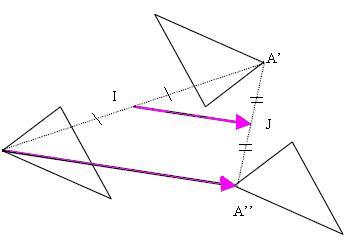
Soient I et J deux points du plan,
la composée de la symétrie de centre I suivie de la symétrie de
centre J est la translation de vecteur ,
que l‘on note .
Preuve :
I milieu de [AA‘] et J milieu de [A‘A‘‘]
On en déduit que d‘après les propriétés de la droite des milieux dans un triangle (étudié en quatrième).
V. Coordonnées dans un repère :
1. Repères :
Trois points non alignés O,I,J ,tels que , définissent un repère du plan. On note souvent
2. Coordonnées d‘un vecteur.
Dans le plan muni d‘un repère ,
si deux points A et B ont pour coordonnées respectives (xA ; yA) et (xB ; yB), alors le vecteur AB a pour coordonnées .
Ces coordonnées correspondent au déplacement horizontal puis vertical pour aller de A à B (affectés de signes).
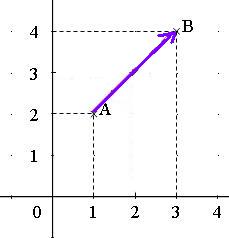
Exemple :
Dans un repère du plan, soient A(1 ; 2) et B(3 ; 4)
donc les coordonnées de sont
.
3. Coordonnées du milieu d‘un segment :
Dans le plan muni d‘un repère ,
si deux points A et B ont pour coordonnées respectives et
,
alors
le milieu M du segment [AB] a pour coordonnées :
.
Exemple :
Dans un repère ,
on donne A(1 ; 2) et B(3 ; 4) :
Conclusion :
Les coordonnées du milieu I du segment [AB] sont (2 ; 3)
Dans le plan muni d‘un repère ,
si deux points A et B ont pour coordonnées respectives et
.
alors la distance entre les deux points A et B se calcule en utilisant la formule :
Attention :
Aucune simplification n‘est possible dans cette formule entre la racine et les carrés .
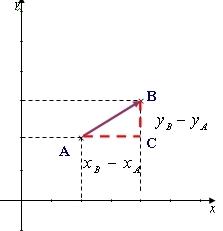
Preuve :
Considérons le triangle ABC de la figure rectangle en C,
d‘après le théorème de Pythagore (étudié en quatrième)
d‘ où
Exemple :
Dans un repère du plan ,
Reprenons l‘exemple précédent avec A(1 ; 2) et B(3 ; 4) :
Conclusion :
La distance AB vaut .
Vous avez assimilé ce cours sur les vecteurs en 2de?
Effectuez ce QCM sur les vecteurs en classe de seconde.
Un QCM sur les vecteurs, translations et coordonnées dans le plan.






 Mathovore c'est 13 931 843 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 931 843 cours et exercices de maths téléchargés en PDF.