Exercice n° 1 :
Déterminer la forme canonique des polynômes suivants :
a.
b.
c.
d.
e.
Exercice n° 2:
Résoudre les équations suivantes dans .
a.
b.
c.
d.
e.
f.
g.
h.
i.
Exercice n° 3 :
Déterminer a et b deux réels tels que :
1.
2.
Exercice n° 4 :
Résoudre dans les inequations suivantes :
a.
b.
c.
d.
e.
Exercice n°5 :
Déterminer le domaine de définition des fonctions suivantes définies par :
a. .
b. .
c. .
Exercice 6 – Equations sous forme de fractions
Résoudre les équations et inéquation suivantes :
1. .
2. .
3. .
Exercice 7 – Résoudre inéquation complexe
Résoudre l’inéquation suivante :
Exercice 8 – Trinôme et équations du second degré
Les questions de cet exercice sont indépendantes.
1. Trouver une fonction polynôme du second degré ayant 1 et 4 comme racines.
Peut-on trouver un tel polynôme dont la courbe représentative passe par le point A(-1 ; 1 )?
Si oui, le donner.
2. Montrer que pour un réel , l’équation
admet deux solutions réelles distinctes.
3. est un réel.On considère l’équation (E) :
.
Pour quelles valeurs de l’équation (E) a-t-elle une unique solution ?
Calculer alors cette solution.
Exercice 9 – Géométrie
Dans un carré de 10 cm de côté, on a colorié une bande de largeur x cm et un carré de côté x cm centré comme sur la figure ci-dessous.
1. Exprimer en fonction de x l’aire de la partie coloriée.On notera A(x) cette aire.
2. Déterminer pour quelle valeurs de x, l’aire coloriée est égale à l’aire de la partie blanche.
Exercice 10 – Equations et inéquations à résoudre
Résoudre les équations et inéquations suivantes :
1.
2.
3.
4.
Exercice 11 – Trouver le périmètre d’un triangle rectangle
L’aire d’un triangle rectangle est 429 m², et l’hypoténuse a pour longueur h = 72,5 m.
Trouver le périmètre.
Exercice 12 – Vitesses de cyclistes
Pour se rendre d’une ville A à une ville B distantes de 195 km, deux cyclistes partent en même temps.
L’un deux, dont la vitesse moyenne sur ce parcours est supérieure à 4 km/h à celle de l’autre, arrive une heure plus tôt.
Quelles sont les vitesses des deux cyclistes ?
Exercice 13 – Problème et équations du second degré
1. On dispose d’une baguette de bois de 10 cm de long.
Où briser la baguette pour que les morceaux obtenus soient deux côtés consécutifs d’un rectangle de surface 20 cm² ?
2. Même question avec un rectangle d’aire 40 cm².
Exercice 14 – Résoudre des inéquations du second degré
Résoudre les inéquations suivantes :
1.
2.
3.
Exercice 15 – Changement de variable
1. Résoudre les équations suivantes :
a. .
b. .
2. Résoudre l’équation suivante : .
Indication : on pourra poser
Exercice 16 – Drapeau rectangulaire
Sur un drapeau rectangulaire de longueur 4 m et de largeur 3 m, on trouve une croix d’épaisseur x m.
Quelle valeur doit-on donner à la largeur de la croix pour que son aire soit égale à la moitié du drapeau ?
Exercice 17 – Résoudre des équations du second degré
Résoudre dans les équations suivantes :
1.
2. .
3. .
4. .
5) .
6)
Exercice 18 – Trouver trois carrés
Peut-on trouver trois carrés ayant pour côtés des entiers consécutifs et dont la somme des aires soit égale à 15 125 ?
Si oui, préciser quelles valeurs doivent avoir les côtés.
Même question avec 15 127.
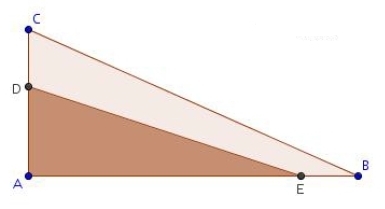
Exercice 19 – Géométrie
Dans un triangle ABC rectangle en A, on place les points D et E respectivement sur [AC] et [AB] tels que
AD = BE = x.
Déterminer x pour que l’aire du triangle ADE soit égale à la moitié de celle du triangle ABC.
On donne : AB = 18 m et AC = 8 m.
Exercice 20 – Résolution d’équations et inéquations
Résoudre :
a.
b.
c.
Exercice 21 – Equations et fractions
Résoudre les équations suivantes :
1.
2.
Exercice 22 – Prix de l’essence
On achète pour 40 € d’essence à une station service.
On s’aperçoit qu’à une autre station, le prix du litre d’essence est inférieur de 0,10 €.
On aurait pu ainsi obtenir 5 litres de plus pour le même prix.
Quel était le prix d’essence à la première station et combien de litres en avait-on pris ?
Exercice 23 – Trouver deux nombres
Trouver deux nombres dont la somme est égale à 57 et le produit égal à 540.
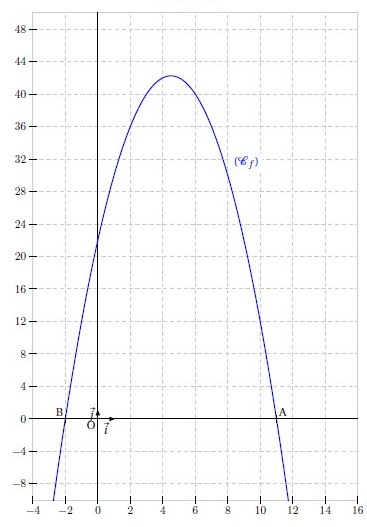
Exercice 24 – Résoudre une inéquation graphiquement et par le calcul
Résoudre l’inéquation suivante :
Résoudre les équations suivantes :
1)
2)
3)
4) .
Exercice 25 – Racines et fonctions du second degré
On considère la fonction définie sur
par
.
1. Déterminer les éventuelles racines de et en déduire, si possible, une factorisation de
.
2. Déterminer les coordonnées des points d’intersection de la courbe de avec les axes du repère.
3. Soit la fonction définie sur
par
.
Etudier la position relative des courbes de et
.
Exercice 26 – Etude d’un trinôme
On donne le trinôme du second degré P défini par :
1. Montrer que P admet pour racine.
2. Trouver l’autre racine (en valeur exacte).
Exercice 27 – Equations du second degré
Résoudre les équations suivantes :
a)
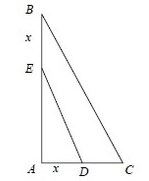
Exercice 28 – Géométrie
Dans un triangle ABC rectangle en A, on place les points D et E respectivement sur [AC] et [AB] tels que AD=BE=x.
Déterminer x pour que l’aire du triangle ADE soit égale à la moitié de celle du triangle ABC.
Données : AB= 18 m et AC = 8 m.















 Mathovore c'est 13 927 700 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 927 700 cours et exercices de maths téléchargés en PDF.
Je souhaiterais avoir des livres de maths corriger