Sommaire de cette fiche
- 1 I. Nombre dérivé – Fonction dérivée – tangente à une courbe.
- 2 II. Fonction dérivable sur un intervalle I. Fonction dérivée d’une fonction dérivable sur I
- 3 III. Équation de la tangente à une courbe
- 4 IV. Signe de la dérivée et sens de variation d’une fonction
- 5 V. Changement de signe de la dérivée et extremum d’une fonction
Dans cette leçon en première, nous aborderons la dérivée d’une somme, d’un produit et d’un quotient. La dérivée et le sens de variation d’une fonction, ainsi que les dérivées des fonctions usuelles.
I. Nombre dérivé – Fonction dérivée – tangente à une courbe.
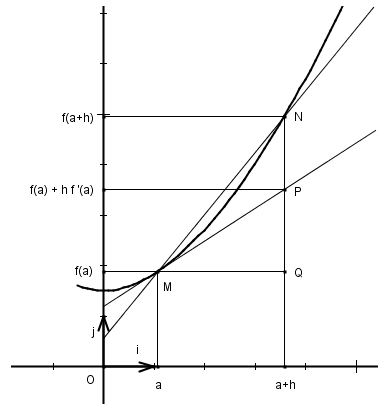
Soit f est une fonction définie sur un intervalle I. La courbe (C) ci-dessous est la représentation graphique de f dans un repère orthonormal .M et N sont deux points de (C) d’abscisses respectives
et
où
.
M et N ont donc pour coordonnées: et
, c’est à dire:
.
On a donc: soit
La droite (MN) sécante à (C) a donc pour coefficient directeur:
.
Si la courbe (C) possède en M une tangente de coefficient directeur d, alors lorsque le point N se rapproche de M, c’est à dire lorsque x tend vers a, ou, ce qui revient au même, lorsque h tend vers 0,
les sécantes (MN) vont atteindre une position limite qui est celle de la tangente(MP) en M à (C).
Ceci peut alors se traduire à l’aide des coefficients directeurs par:
, c’est à dire :
.
On a donc: .
Si nous appelons , la fonction définie pour
et
par :
.
on a :
et
, ce qui s’écrit aussi:
.
Réciproquement, s’il existe un réel d et une fonction telle que, pour tout
et
, on ait:
avec
,
on en déduit que: et donc que:
.
Ceci nous permet donc de donner les trois définitions équivalentes:
Si f est une fonction définie sur un intervalle et si
.
Lorsqu’il existe un nombre réel d tel que, pour tout réel h proche de 0, on ait
On dit que la fonction f est dérivable en a et que est le nombre dérivé de f en a.
Si f est une fonction définie sur un intervalle I et si .
Lorsqu’il existe un nombre réel d tel que, pour tout réel et proche de a, on ait:
On dit que la fonction f est dérivable en a et que est le nombre dérivé de f en a.
II. Fonction dérivable sur un intervalle I. Fonction dérivée d’une fonction dérivable sur I
On dit que f est dérivable sur un intervalle I lorsqu’elle est dérivable en tout point de I.
Lorsque f est dérivable sur un intervalle I, la fonction qui à tout associe le nombre dérivé de f en x est appelée fonction dérivée de f sur I. Cette fonction est notée
.
Si f est une fonction définie sur un intervalle I. Si et si f est dérivable en
, alors :La courbe représentative de f possède une tangente au point
et le coefficient directeur de cette tangente est le nombre dérivé
de la fonction f en
.
Remarques :
Si le graphique de f ne possède pas de tangente au point M d’abscisse , alors la fonction f n’est pas dérivable en a. C’est le cas de la fonction valeur absolue en
.
Le graphique d’une fonction peut fort bien posséder une tangente en un point sans que la fonction soit dérivable en ce point : il suffit que le coefficient directeur de cette tangente n’existe pas (tangente parallèle à l’axe des ordonnées).
C’est le cas de la fonction racine carrée en .
III. Équation de la tangente à une courbe
Si fonction f est dérivable en a, la tangente (MP) à la courbe (C) en M d’abscisse existe.Elle a pour coefficient directeur
.
Son équation est donc de la forme: , où
et son ordonnée à l’origine p peut être calculée.
Il suffit d’écrire que (MP) passe par .
On a donc: . Ceci donne:
.
Donc: que l’on écrit souvent sous l’une des formes, plus faciles à retenir:
Equation de la tangente au point :
ou
.
IV. Signe de la dérivée et sens de variation d’une fonction
Nous admettrons sans démonstration les théorèmes suivants:
Soit f est une fonction dérivable sur un intervalle I.
- Si f est croissante sur I, alors pour tout
, on a:
- Si f est décroissante sur I, alors pour tout
, on a:
.
- Si f est constante sur I, alors pour tout
, on a:
.
Soit f est une fonction dérivable sur un intervalle I.
- Si, pour tout
, on a:
, alors f est croissante sur I.
- Si, pour tout
, on a:
, alors f est décroissante sur I.
- Si, pour tout
, on a:
, alors f est constante sur I.
Soit f est une fonction dérivable sur un intervalle I.
- Si, pour tout
, on a:
( sauf peut-être en des points isolés où
),alors f est strictement croissante sur I.
- Si, pour tout
, on a:
( sauf peut-être en des points isolés où
),alors f est strictement décroissante sur I.
En particulier:
Soit f une fonction dérivable sur un intervalle .
- Si, pour tout
, on a
, alors f est strictement croissante sur
.
- Si, pour tout
, on a
, alors f est strictement décroissante sur
.
Exemples :
1) Soit la fonction f définie sur par
.
f est dérivable sur et
pour tout
.
· Pour tout , on a
, donc f est décroissante sur
.
· Pour tout, on a
, donc f est croissante sur
.
Bien que , on a de façon plus précise :
· Pour tout , on a
, donc f est strictement décroissante sur
.
· Pour tout , on a
, donc f est strictement croissante sur
.
V. Changement de signe de la dérivée et extremum d’une fonction
Nous admettrons sans démonstration les théorèmes suivants:
Si f est une fonction dérivable sur un intervalle I,
Et si f admet un maximum local ou un minimum local en différent des extrémités de l’intervalle I,
Alors: .
1.Cas particulier où f est dérivable sur un intervalle ouvert.
Si f est une fonction dérivable sur un intervalle ouvert I,
Et si f admet un maximum local ou un minimum local en ,
Alors: .
Si f est une fonction dérivable sur un intervalle ouvert I,
et si et si
s’annule pour
en changeant de signe,
Alors f(a) est un extremum local de f sur I.
Exemples :
1) Soit la fonction f définie sur par
. f est dérivable sur
avec
.
s’annule en
et
en changeant de signe, car :
- pour x appartenant à
, on a :
donc f est strictement croissante sur
- .
- pour x appartenant à
, on a :
donc f est strictement décroissante sur
.
- pour x appartenant à
, on a :
donc f est strictement croissante sur
.
La fonction possède donc un maximum local en
et un minimum local en
.
Toute cette étude peut être résumée dans le tableau ci-dessous :
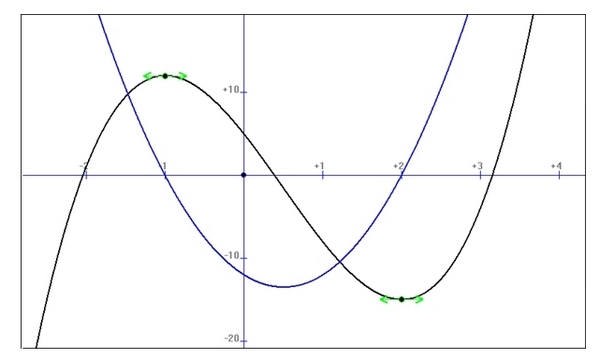
Voici un morceau des représentations graphiques de f et de :







 Mathovore c'est 13 929 592 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 929 592 cours et exercices de maths téléchargés en PDF.