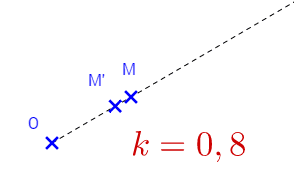Homothéties : cours de maths en 3ème à télécharger en PDF.

Sommaire de cette fiche

1 I. L’homothétie

Les homothéties dans un cours de maths en 3ème où nous aborderons la définition d’une homothétie de rapport k, de l’image d’un point ainsi que ses différentes propriétés (conservation de l’alignement, multiplication des longueurs et des aires).

Dans cette leçon en troisième, nous construirons à la règle est au compas l’image ou encore le centre d’une homothétie de rapport k non nul.

I. L’homothétie

1.Introduction

Définition

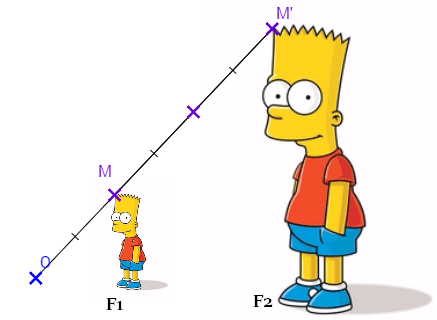
La figure est un agrandissement de rapport 3 de la figure .
On dit que la figure est l’image de la figure par l’homothétie de centre O et de rapport 3.
La figure est une réduction de la figure de rapport $\frac{1}{3}$ .
On dit que la figure est l’image de la figure par l’homothétie de centre O et de rapport $\frac{1}{3}$ .

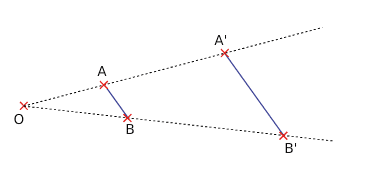
2. image d’un point

Définition

L’image d’un point M par l’homothétie de centre O et de rapport k positif est le point M’ tel que :

M’ appartient à la demi-droite [OM);
${\color{DarkRed}\,OM'=k\times \,OM}$

Exemples :

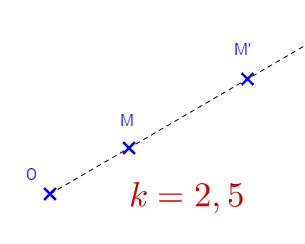
Construire l’image du point M par l’homothétie de rapport k = 2,5 puis k = 0,8.

Remarque :

Dans le cas où , les images sont confondues avec les points de départs.

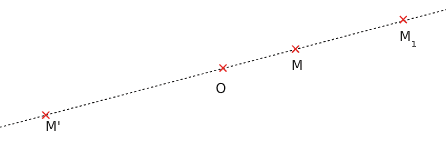
Dans le cas où , par exemple , on construit l’image de M

par l’homothétie de centre O et de rapport 2 puis on construit le symétrique M’ de par rapport à O.

3. Image d’un segment

Propriété :

On considère A,B et O trois points du plan et k un nombre positif.

Si les points A’ et B’ sont les images respectives des points A et B

par l’homothétie de centre O et de rapport k

alors :

$\star\,\,A'B'=k\times \,AB$

$\star\,\,(AB)//(A'B')$

Démonstration :

Par définition de l’homothétie de centre O et de rapport k, nous avons :

$OA'=k\times \,OA$ et $OB'=k\times \,OB$ donc $\frac{OA'}{OA}=\frac{OB'}{OB}=k$

Ainsi en utilisant la réciproque du théorème de Thalès, nous en déduisons

que les droites (AB) et (A’B’) sont parallèles.

Ensuite, nous pouvons appliquer la partie directe du théorème de Thalès.

On sait que : $A\in(OA'),\,B\in\,(OB'),(AB)//(A'B')\,.$

donc nous avons les égalités suivantes :

$\frac{A'B'}{AB}=\frac{OA'}{OA}=\frac{OB'}{OB}=k$ ainsi ${\color{DarkRed}\,A'B'=k\times \,AB\,}$ .

4. Les propriétés des homothéties

Propriété :

L’homothétie conserve l’alignement, les milieux et la mesure des angles.

Propriété :

Dans une homothétie de rapport k positif :

les longueurs sont multipliées par k;
les aires sont multipliées par k².

Propriété :

On considère la figure qui est l’image de la figure par une homothétie de centre O et de rapport k.

Si alors est un agrandissement de par cette homothétie;
Si alors est une réduction de par cette homothétie.

Exemple :

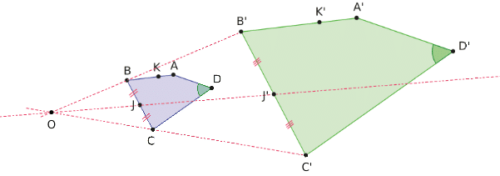
Le quadrilatère A’B’C’D’ est l’image du quadrilatère ABCD par l’homothétie de centre O et de rapport .

Les points A,B,K sont alignés donc leurs images respectives A’,B’,K’ sont alignées;
Le point J est le milieu de [BC] donc son image J’ est le milieu du segment [B’C’];
L’angle $\widehat{A'D'C'}$ est l’image de l’angle $\widehat{ADC}$ , ils ont donc la même mesure;
Les longueurs sont multipliées par 2,1 ainsi $B'C'=2,1\times \,BC$ ;
Les aires sont multipliées par ainsi $Aire_{A'B'C'D'}=4,41\times \,Aire_{ABCD}$ .

4.2/5 - (12 votes)

Télécharger et imprimer ce document en PDF gratuitement

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «homothéties : cours de maths en 3ème» au format PDF.

Télécharger nos applications gratuites avec tous les cours,exercices corrigés.

D'autres fiches similaires à homothéties : cours de maths en 3ème.

Mathovore vous permet de réviser en ligne et de progresser en mathématiques tout au long de l'année scolaire.
De nombreuses ressources destinées aux élèves désireux de combler leurs lacunes en maths et d'envisager une progression constante. Tous les cours en primaire, au collège, au lycée mais également, en maths supérieures et spéciales ainsi qu'en licence sont disponibles sur notre sites web de mathématiques.
Des documents similaires à homothéties : cours de maths en 3ème à télécharger ou à imprimer gratuitement en PDF avec tous les cours de maths du collège au lycée et post bac rédigés par des enseignants de l'éducation nationale.
Vérifiez si vous avez acquis le contenu des différentes leçons (définition, propriétés, téhorèmpe) en vous exerçant sur des milliers d'exercices de maths disponibles sur Mathovore et chacun de ces exercices dispose de son corrigé.
En complément des cours et exercices sur le thème homothéties : cours de maths en 3ème, les élèves de troisième pourront réviser le brevet de maths en ligne ainsi que pour les élèves de terminale pourront s'exercer sur les sujets corrigé du baccalauréat de maths en ligne.

Les dernières fiches mises à jour

Voici les dernières ressources mis à jour sur Mathovore (des cours, exercices, des contrôles et autres), rédigées par notre équipe d'enseignants.

Mathovore c'est 2 365 024 cours et exercices de maths téléchargés en PDF et 181 073 membres.
Rejoignez-nous : inscription gratuite.