Exercice 1 : (13 points)
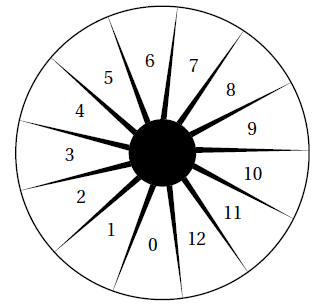
On considère un jeu composé d’un plateau tournant et d’une boule.
Représenté ci-dessous, ce plateau comporte 13 cases numérotées de 0 à 12.
On lance la boule sur le plateau, La boule finit par s’arrêter au hasard sur une case numérotée.
La boule a la même probabilité de s’arrêter sur chaque case.
1. Quelle est la probabilité que la boule s’arrête sur la case numérotée 8?
2. Quelle est la probabilité que le numéro de la case sur lequel la boule s’arrête soit un nombre impair ?
3. Quelle est la probabilité que le numéro de la case sur laquelle la boule s’arrête soit un nombre
premier ?
4. Lors des deux derniers lancers, la boule s’est arrêtée à chaque fois sur la case numérotée 9.
A-t-on maintenant plus de chances que la boule s’arrête sur la case numérotée 9 plutôt que sur
la case numérotée 7?
Argumenter à l’aide d’un calcul de probabilités.
Exercice 2 : (9 points)
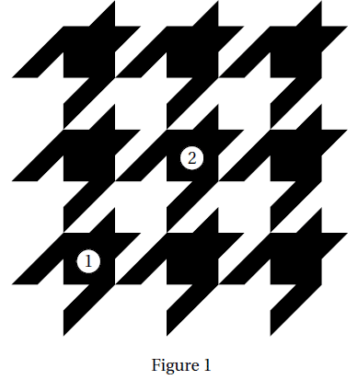
Le pavage représenté sur la figure 1 est réalisé à partir d’un motif appelé pied-de-coq qui est présent
sur de nombreux tissus utilisés pour la fabrication de vêtements.
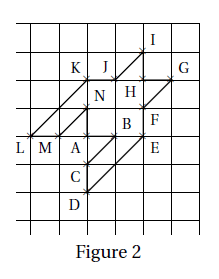
Le motif pied-de-coq est représenté par le polygone ci-dessous à droite (figure 2) qui peut être réalisé
à l’aide d’un quadrillage régulier.
1. Sur la figure 1, quel type de transformation géométrique permet d’obtenir le motif 2 à partir du
motif 1?
2. Dans celte question, on considère que : AB = 1 cm(figure 2).
Déterminer l’aire d’un motif pied-de-coq.
3. Marie affirme « si je divise par 2 les longueurs d’un motif, son aire sera aussi divisée par 2 ».
A-t-elle raison? Expliquer pourquoi.
Exercice 3 : (9 points)
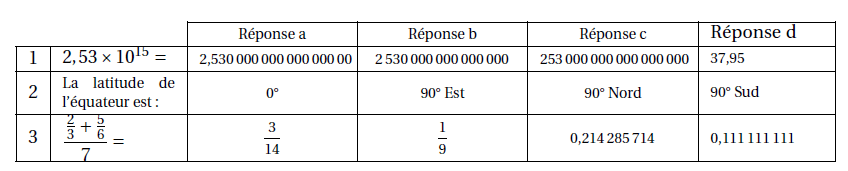
Cet exercice est un Q. C.M. (Questionnaire à choix multiples).
Pour chacune des questions, quatre réponses sont proposées et une seule est exacte. Une réponse
fausse ou absente n’enlève pas de point.
Pour chacune des trois questions, écrire sur votre copie le numéro de la question et la lettre correspondant à la bonne réponse.
Exercice 4 : (18 points)
1. Corinne choisit le nombre 1 et applique le programme A.
Expliquer en détaillant les calculs que le résultat du programme de calcul est 4.
2. Tidjane choisit le nombre −5 et applique le programme B. Quel résultat obtient-il ?
3. Lina souhaite regrouper le résultat de chaque programme à l’aide d’un tableur. Elle crée la
feuille de calcul ci-dessous. Quelle formule, copiée ensuite à droite dans les cellules C3 à H3,
a-t-elle saisie dans la cellule B3?
4. Zoé cherche à trouver un nombre de départ pour lequel les deux programmes de calcul donnent
le même résultat. Pour cela, elle appelle x le nombre choisi au départ et exprime le résultat de
chaque programme de calcul en fonction de x.
a. Montrer que le résultat du programme A en fonction de x peut s’écrire sous forme développée
et réduite : x² −6x +9,
b. Écrire le résultat du programme B.
c. Existe-t-il un nombre de départ pour lequel les deux programmes donnent le même résultat
?
Si oui, lequel ?
Exercice 5 : (20 points)
Dans tout l’exercice l’unité de longueur est le mm.
On lance une fléchette sur une plaque carrée sur laquelle figure une cible circulaire (en gris sur la figure), Si la pointe de la fléchette est sur le bord de la cible, on considère que la cible n’est pas atteinte.
On considère que cette expérience est aléatoire et l’on s’intéresse à la probabilité que la fléchette atteigne la cible.
— La longueur du côté de la plaque carrée est 200.
— Le rayon de la cible est 100.
— La fléchette est représentée par le point F de coordonnées (x ; y) où x et y sont des nombres aléatoires compris entre −100 et 100.
1. Dans l’exemple ci-dessus, la fléchette F est située au point de coordonnées (72; 54).
Montrer que la distance OF, entre la fléchette et l’origine du repère est 90.
2. D’une façon générale, quel nombre ne doit pas dépasser la distance OF pour que la fléchette
atteigne la cible?
3. On réalise un programme qui simule plusieurs fois le lancer de cette fléchette sur la plaque
carrée et qui compte le nombre de lancers atteignant la cible. Le programmeur a créé trois
variables nommées : carré de OF, distance et score.
a. Lorsqu’on exécute ce programme, combien de lancers sont simulés ?
b. Quel est le rôle de la variable score?
c. Compléter et recopier sur la copie uniquement les lignes 5, 6 et 7 du programme afin qu’il
fonctionne correctement.
d. Après une exécution du programme, la variable score est égale à 102.
À quelle fréquence la cible a-t-elle été atteinte dans cette simulation?
Exprimer le résultat sous la forme d’une fraction irréductible.
4. On admet que la probabilité d’atteindre la cible est égale au quotient : aire de la cible divisée
par aire de la plaque carrée.
Donner une valeur approchée de cette probabilité au centième près.
Exercice 6 : (15 points)
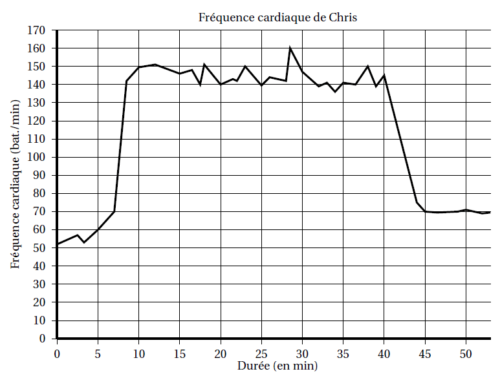
Chris fait une course à vélo tout terrain (VTT). Le graphique ci-dessous représente sa fréquence cardiaque (en battements par minute) en fonction du temps lors de la course.
1. Quelle est la fréquence cardiaque de Chris au départ de sa course?
2. Quel est le maximum de la fréquence cardiaque atteinte par Chris au cours de sa course?
3. Chris est parti à 9 h 33 de chez lui et termine sa course à 10 h 26.
Quelle a été la durée, en minutes de sa course?
4. Chris a parcouru 11 kmlors de cette course.
Montrer que sa vitesse moyenne est d’environ 12,5 km/h.
5. On appelle FCM (Fréquence Cardiaque Maximale) la fréquence maximale que peut supporter
l’organisme. Celle de Chris est FCM= 190 battements parminute.
En effectuant des recherches sur des sites internet spécialisés, il a trouvé le tableau suivant :
Estimer la durée de la période pendant laquelle Chris a fourni un effort soutenu au cours de sa
course.
Exercice 7 : (16 points)
La figure ci-dessous n’ est pas à l’échelle.
On considère ci-dessus un triangle ABC rectangle en A tel que 
et AB = 7 cm. H est le pied
de la hauteur issue de A.
1. Tracer la figure en vraie grandeur sur la copie. Laisser les traits de construction apparents sur la
copie.
2. Démontrer que AH = 3,5 cm.
3. Démontrer que les triangles ABC et HAC sont semblables.
4. Déterminer le coefficient de réduction permettant de passer du triangle ABC au triangle HAC.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2018 à Pondichéry : sujet et corrigé en PDF» au format PDF.
Réviser les leçons et les exercices avec nos Q.C.M :
D'autres utilitaires pour progresser en autonomie :
