Un sujet de brevet de maths 2017 blanc avec des probabilités, des fonctions, de la programmation avec scratch.Des statistiques et un qcm en 3ème.
BREVET BLANC DE MATHEMATIQUES 2017
Durée de l’épreuve : 2 heures
Il sera tenu compte de la qualité de la rédaction et de la présentation (5 points).
L’usage de la calculatrice est autorisé.
Les exercices peuvent être traités dans n’importe quel ordre.
Toutes les réponses doivent être justifiées, sauf si une indication contraire est donnée.
Pour chaque question, si le travail n’est pas terminé, laisser tout de même une trace de la recherche ; elle sera prise en compte dans la notation.
Les exercices 2 et 4 portent sur le thème « L’ÉNERGIE ÉOLIENNE ».
Exercice 1 (4 points) :
Charlotte possède entre 400 et 450 livres. Elle décide de les revendre sur internet pour en acheter d’autres. Elle observe qu’elle peut regrouper tous ses livres par paquets de 3. Elle constate qu’elle peut également le faire par paquets de 5 et aussi par paquets de 7.
Combien de livres Charlotte possède-t-elle exactement ?
Exercice 2 (6,5 points) :
Les questions 1 et 2 peuvent être traitées indépendamment l’une de l’autre.
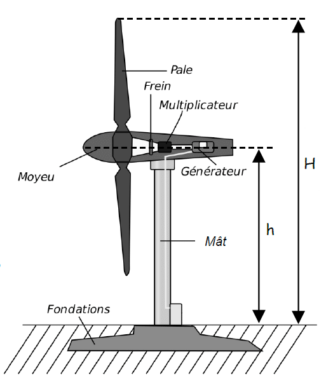
Le schéma ci-dessous est celui d’une éolienne dont la hauteur réelle maximale, notée H, est de 90 m et dont le centre du moyeu est placé à 60 m du sol (distance notée h).
La puissance maximale théorique d’une éolienne est calculée, en watts, par la formule :
où S est la surface en m² du disque balayée par les pales et v est la vitesse du vent en m/s.
1. On s’intéresse ici à l’éolienne en taille réelle :
a. Montrer que la surface S du disque balayée par les pales est égale à .
b. En déduire la puissance maximale théorique, au kilowatt près, pour une vitesse de 20 m/s.
2. On souhaite à présent réaliser une maquette de l’éolienne à l’échelle :
a. Calculer la longueur d’une pale de la maquette.
b. Calculer la puissance maximale théorique de la maquette, au watt près, pour une vitesse de 10 m/s.
Exercice 3 (4 points) :
Dans le premier pot on a mis 5 bonbons au chocolat noir et 3 au chocolat blanc. Dans le second pot on a mis 7 bonbons au chocolat noir et 4 au chocolat blanc. Les bonbons sont indiscernables au toucher.
Si on choisit sans regarder un bonbon dans un des deux pots, dans lequel a-t-on le plus de chances d’en obtenir un au chocolat blanc ? Justifier la réponse.
Exercice 4 (4,5 points) :
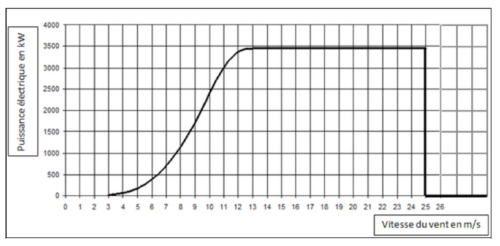
Le graphique ci-dessous donne la puissance (exprimée en kW) délivrée par une éolienne selon la vitesse du vent (exprimée en m/s).
Répondre aux questions suivantes avec la précision permise par le graphique.
1. Pour quelles vitesses du vent l’éolienne produit-elle de l’électricité ?
2. Quelle est la puissance maximale délivrée par l’éolienne ?
3. La vitesse du vent augmente jusqu’à 100 km/h.
Expliquer par une phrase ce qui se passe.
Exercice 5 (5 points) :
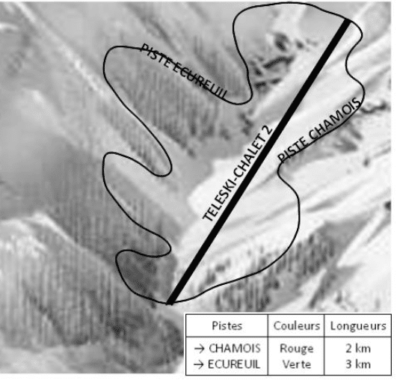
Nina est aux Estables pour une « sortie-ski » avec sa classe. Elle est en bas du TELESKI « Chalet 2 » où personne n’attend.
Il est 16h50 et son professeur a donné rendez-vous au pied des pistes à 17h précises pour le retour. Nina descend en moyenne à 15 km/h.
A-t-elle le temps de faire une dernière descente si elle empreinte l’une de ces deux pistes ?
Exercice 6 (7 points) :
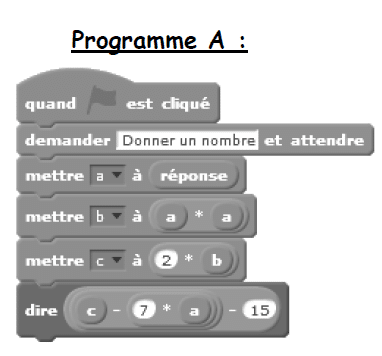
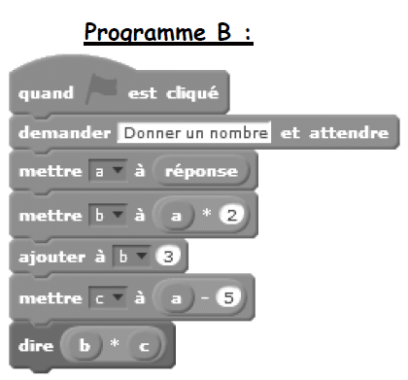
Voici deux programmes réalisés avec scratch.
1. Montrer que le lutin dira 15 dans les deux cas si on répond 6 à la question de départ de chacun des deux programmes.
2. Quel(s) nombre(s) dira-t-il si on répond (-3) à la question de départ de chacun des deux programmes ?
3. Pour n’importe quel même nombre choisi au départ, montrer que les deux programmes donnent des résultats identiques.
Exercice 7 (7 points) :
Un fournisseur d’électricité veut modifier sa tarification. Le montant de la facture annuelle d’un client est la somme du prix de l’abonnement choisi et de sa consommation d’électricité. Le fournisseur désire baisser le prix du kWh de 2 % et augmenter le prix des abonnements de 3% pour l’année 2018 par rapport à 2017.
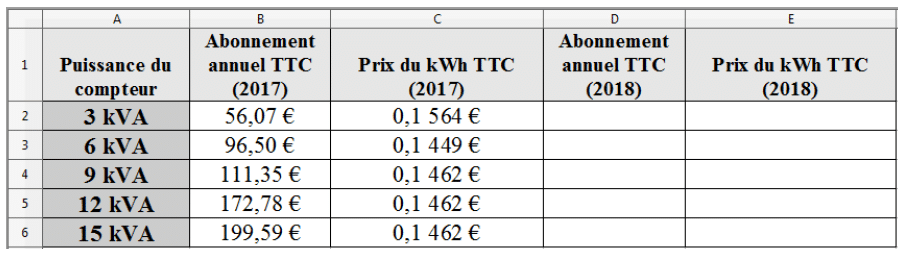
1. Le fournisseur utilise la feuille de calculs ci-dessous pour calculer les prix de l’abonnement et du kWh pour l’année 2018.
a. Pour calculer les montants des abonnements pour 2018, quelle formule peut-il saisir dans la cellule D2 avant de la recopier sur la colonne D ?
b. Pour calculer le prix du kWh pour 2018, quelle formule peut-il saisir dans la cellule E2 avant de la recopier sur la colonne E ?
2. Calculer l’étendue ainsi que la valeur moyenne de l’abonnement annuel TTC en 2017.
3. Paul possède un compteur d’une puissance de 6 kVA et a consommé 5 361 kWh en 2017.
a. Quel est le montant, arrondi au centime, de sa facture d’électricité pour l’année 2017 ?
b. Si sa consommation reste identique, quelle serait le montant, arrondi au centime, de sa facture d’électricité pour l’année 2018 ?
Exercice 8 (7 points) :
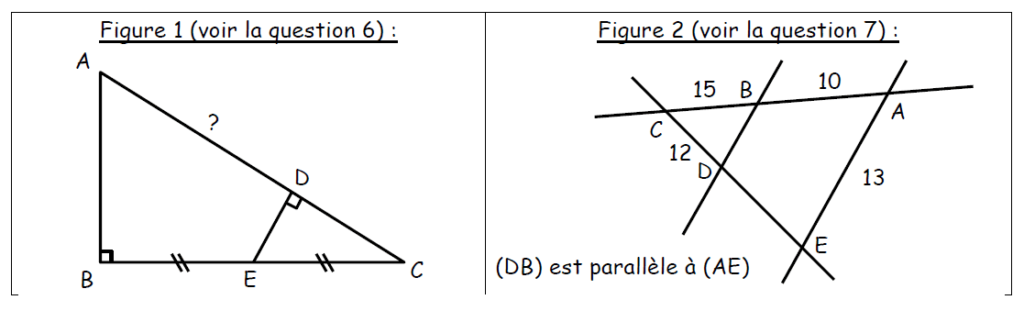
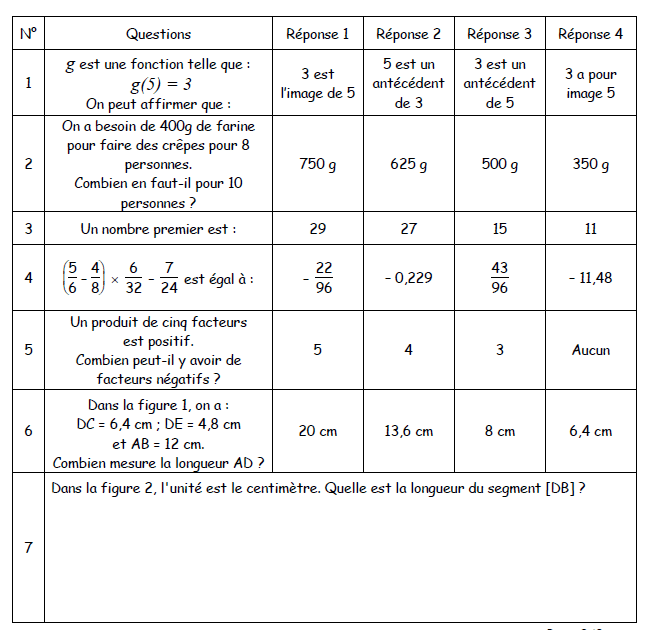
Les questions 1 à 6 sont à choix multiples.
Pour chacune, une ou plusieurs réponses sont justes.
Entourer la ou les réponses sans justifier.
La réponse à la question 7 doit par contre être justifiée dans le cadre prévu à cet effet.



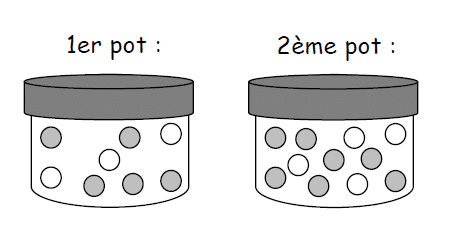




 Mathovore c'est 13 927 695 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 927 695 cours et exercices de maths téléchargés en PDF.