cours maths 2de



Mis à jour le 10 mars 2025

Variations de fonctions et extremums : cours de maths en 2de en PDF.

par
 Les variations de fonctions et les extremums à travers un cours de maths en 2de avec la croissance et décroissance d’une fonction ainsi que le tableau de variation. Nous étudierons, dans cette leçon en seconde,  l’aspect algébrique puis l’aspect graphique de l’étude des variations.
Les connaissances de collège nécessaires pour aborder cette fiche sont les suivantes :

  • Calculer l’image d’un nombre par une fonction;
  • Lire une image par une fonction sur un graphique;
  • Reconnaître une fonction affine;
  • Connaître les effets des opérations sur l’ordre des nombres.

I. Point de vue graphique

1. Fonction croissante, décroissante, constante

Définition :
On dit que f est croissante sur un intervalle I lorsque si x augmente sur I alors f (x) augmente.
On dit que f est décroissante sur un intervalle I lorsque si x augmente sur I alors f (x) diminue.

Fonction croissante ou décroissante et variations de fonctions

Définition :

Soit f une fonction et C_f sa courbe représentative dans un repère.
On voit sur un graphique que :

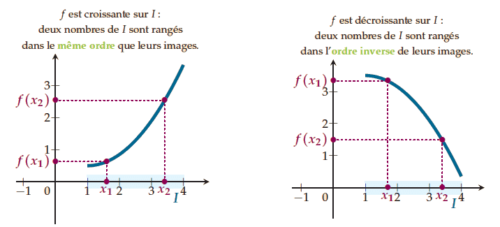
  • f est croissante sur I lorsque Cf «monte » sur I ;
  • f est décroissante sur I lorsque Cf « descend » sur I.
  • Lorsque sur un intervalle, la courbe est horizontale,on dit que la fonction est constante. On considère qu’elle est à la fois croissante et décroissante.
    Une fonction qui ne change pas de sens de variations sur un intervalle est dite monotone sur cet intervalle.

2. Maximum et minimum d’une fonction

Définition :

Sur un intervalle I,

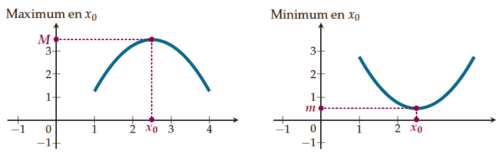
  • le maximum d’une fonction f est la plus grande des valeurs prises par f (x) ;
  • le minimum d’une fonction f est la plus petite des valeurs prises par f (x).

Minimum et maximum d'une fonction

3. Tableau de variation d’une fonction et variations

Définition :

Un tableau de variations regroupe toutes les informations concernant les variations d’une
fonction numérique sur son domaine de définition.

Méthode : dresser un tableau de variation

Un tableau de variations comporte deux lignes.

  •  Aux extrémités de la première ligne, on trouve les bornes du domaine de définition de la fonction.
    Entre les bornes, on place d’éventuelles valeurs particulières.
  • Le sens de variation de la fonction est indiqué sur la deuxième ligne par une ou plusieurs flèches sur les intervalles où elle est monotone : croissante  pour croissante et décroissante pour décroissante.
  • Les valeurs pour lesquelles la fonction n’est pas définie sont indiquées par une double
    barre verticale sur la deuxième ligne.
  • On indique au bout des flèches les images des valeurs de la première ligne.

Exemple :

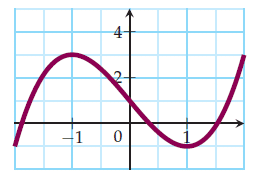
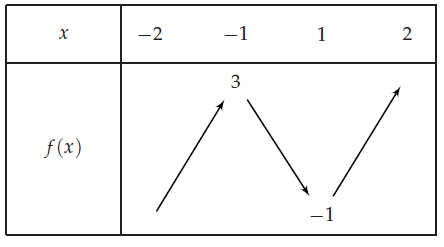
Dresser le tableau de variations de la fonction définie sur [−2; 2] par la courbe ci-dessous.

Exemple de courbe

Voici le tableau de variation correspondant :

Tableau de variation

II. Point de vue algébrique

1.Variation d’une fonction

Définition : croissance, décroissance sur un intervalle.

Soit f une fonction définie sur un intervalle I et x_1 et x_2 deux nombres de I.
Si x_1\leq\,\,x_2  implique f(x_1)\leq\,\,f(x_2) alors f est dite croissante sur I.
Si x_1\,\geq\,\,x_2  implique f(x_1)\,\geq\,\,f(x_2)  alors f est dite décroissante sur I.

Variation d'une fonction

Propriété : tableau de variations des fonctions affines et de la fonction inverse.
Le sens de variation de la fonction affine dépend du signe de a.
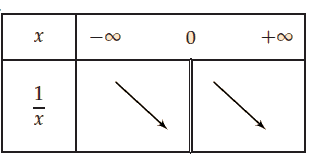
La fonction inverse est décroissante sur R^{-*} et sur R^{+*}.

Tableau de variation des fonctions affines

Tableau de variation des fonctions affines

Démonstration :
On considère une fonction f tel que f (x) = ax + b et deux nombres tels que x_1<x_2.
Si a<0;\,ax_1>ax_2 et f(x_1)\,>\,f(x_2). La fonction f est donc décroissante sur R.
Sia<0;\,ax_1<ax_2 et f(x_1)<\,f(x_2). La fonction f est donc croissante sur R.

Tableau de variation de la fonction inverse

Tableau de variation de la fonction inverse

2. Maximum et minimum d’une fonction

Définition : maximum, minimum et extremum d’une fonction
  • Dire que f admet un maximum en a sur l’intervalle I signifie que :

Il existe un réel M tel que pour tout x dans I : f(x)\leq\,\,M et M=f(a);

  • Dire que f admet un minimum en b sur l’intervalle I signifie que :
    Il existe un réel m tel que pour tout x dans I : f(x)\,\geq\,\,m et m=f(b) ;
  • Un extremum est le terme générique pour désigner un maximum ou un minimum.

Maximum et minimum : aspect graphique.

Propriété : tableau de variations de la fonction carrée.
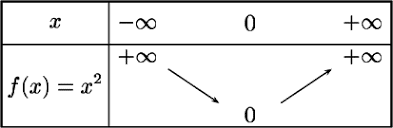
  • La fonction carrée est décroissante sur R^{-} et croissante sur R^{+}.
  • Elle admet, sur R, un minimum en 0.

tableau variation fonction carrée

3.3/5 - (35 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «variations de fonctions et extremums : cours de maths en 2de en PDF.» au format PDF.

D'autres cours et exercices à consulter

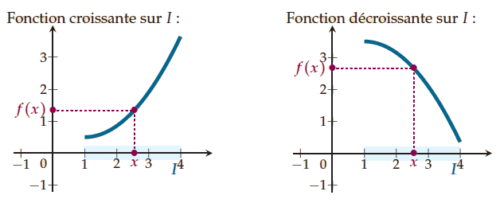
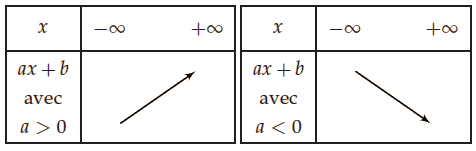
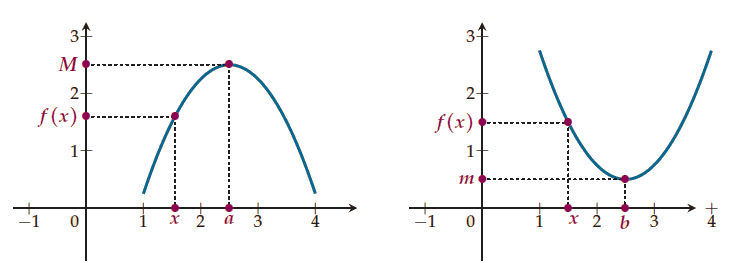
Inscription gratuite à Mathovore.  Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

✕
Mathovore

GRATUIT
VOIR