Sommaire de cette fiche
0. Introduction :un peu d’histoire
Le mot vient du grec « trigone » (triangle) et « metron » (mesure).Dans l‘Encyclopédie (1751), Jean le Rond d‘Alembert (1717 ; 1783) définit la trigonométrie comme :
« l‘art de trouver les parties inconnues d‘un triangle par le moyen de celles qu‘on connaît ».
C‘est bien la démarche qui est demandée aux élèves du collège.
I. Relations trigonométriques dans le triangle rectangle :
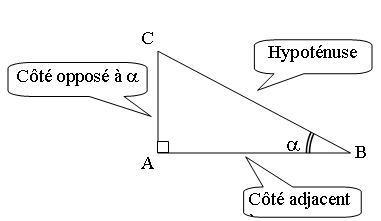
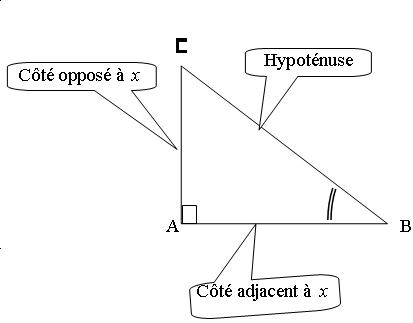
Dans un triangle rectangle ABC, on peut définir les relations suivantes entre les angles aigus et les différentes longueurs des côtés.
– Le cosinus d’un angle aigu est donné par:
– Le sinus d’un angle aigu est donné par :
– La tangente d’un angle aigu est donnée par :
Explications:
CAH: Cos()= (longueur du cote Adjacent a l’angle
) : (longueur de l’Hypotenuse )
SOH: Sin()= (longueur du cote Opposé a l’angle
) : (longueur de l’Hypotenuse )
TOA: Tan()= (longueur du cote Opposé a l’angle
): (longueur du cote Adjacent a l’angle
)
Remarques :
– Le sinus et le cosinus d‘un angle sont toujours compris entre – 1 et 1.
– Par contre, la tangente d‘un angle aigu peut prendre toutes les valeurs.
Exemples :
Si AC=16 cm et BC=20 cm, calculer .
[ Réponse : =0,8]
Si AC=16 cm et AB= 12 cm, calculer
[ Réponse : =1,33]
II. Détermination de la mesure d’un angle en degré, connaissant son cox ou sin x ou tan x :
La détermination de la mesure d‘un angle connaissant son cos x, sin x ou tan x s‘effectue à l‘aide de la calculatrice en utilisant les touches :
En ayant vérifié, préalablement, que la calculatrice est en mode degré
Exemples :
Si cos x = 0,5 alors
Si sin x = 0,5 alors
Si tan x = 1 alors
III. Formules Trigonométriques :
Pour tout angle x, les égalités suivantes sont toujours vraies :
Preuve :
Or ABC est rectangle en A, donc d‘après la partie directe du théorème de Pythagore : AB²+AC²=BC²
D’où :
Puis
Vous avez assimilé le cours sur la trigonométrie en 3ème ?
Effectuez ce QCM sur la trigonométrie dans le triangle rectangle afin d’évaluer vos acquis sur cette leçon en troisième.
Résumé-Quiz
0 questions correctes sur 10
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
QCM sur la trigonométrie dans le triangle rectangle en troisième.
Vous avez déjà rempli le questionnaire avant. Par conséquent, vous ne pouvez pas recommencer.
Quiz is loading...
You must sign in or sign up to start the quiz.
Vous devez finir le quiz suivant, avant de commencer celui-ci :
Résultats
0 questions sur 10 répondues correctement
Votre temps:
Temps écoulé
Vous avez atteint 0 points sur 0 , (0)
| Score moyen |
|
| Votre score |
|
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Répondu
- Examiner
-
Question 1 sur 10
Soit PIC un triangle rectangle en P.
Le côté opposé à l’angle
est :
Exact
Inexact
-
Question 2 sur 10
Soit ROI un triangle rectangle dont l’hypoténuse est [RO].
Le coté adjacent à l’angle
est
Exact
Inexact
-
Question 3 sur 10
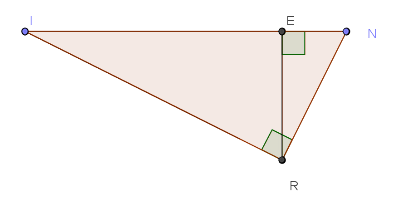
Soit la figure ci-dessous :
Le rapport égal à
est :
Exact
Inexact
-
Question 4 sur 10
Soit la figure ci-dessous :
L’égalité correcte est :
Exact
Inexact
-
Question 5 sur 10
Soit la figure ci-dessous :
La longueur RE est égale à
Exact
Inexact
-
Question 6 sur 10
Soit TAN un triangle rectangle en T.
L’égalité correcte est :
Exact
Inexact
-
Question 7 sur 10
Soit trois angles
.
L’égalité correcte est :
Exact
Inexact
-
Question 8 sur 10
L’égalité correcte est :
Exact
Inexact
-
Question 9 sur 10
Soit SUD un triangle rectangle en S tel que DU = 4 cm et
.
Une valeur approchée à 0,1 cm près de la longueur DS est :
Exact
Inexact
-
Question 10 sur 10
Soit EST un triangle rectangle en S tel que ES = 6 cm et ST = 5 cm.
Une valeur approchée au dixième de degré près de l’angle
est :
Exact
Inexact






 Mathovore c'est 13 927 327 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 927 327 cours et exercices de maths téléchargés en PDF.