Signaler une erreur / Remarque ?
Sommaire de cette fiche
I. Section d’un prisme droit par un plan.
- La section d’un prisme droit par un plan parallèle à une base est un polygone de mêmes dimensions que la base.
- La section d’un prisme droit par un plan parallèle à une arête latérale est un rectangle dont une dimension est la longueur de l’arête.
1.Cas particuliers du parallélépipède rectangle
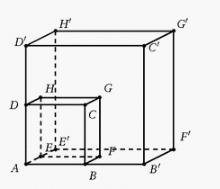
La section par ce plan parallèle à la face ADHE est le rectangle IJKL et IJ=AD et IL=AE.
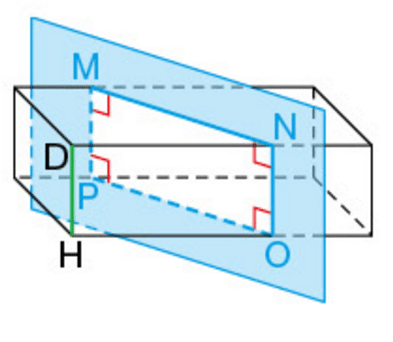
La section par ce plan parallèle à l’arête [DH] est le rectangle MNOP et MP=DH.
II. Section d’un cylindre par un plan.
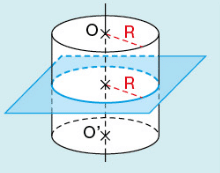
- La section d’un cylindre par un plan parallèle à une base est un cercle de même rayon que la base.
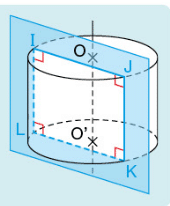
- La section d’un cylindre par rapport à un plan parallèle à son axe est un rectangle dont l’une des dimensions est la hauteur du cylindre.
III. Section d’un cône et d’une pyramide par un plan.
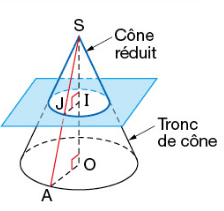
La section d’un cône par un plan parallèle à la base est un cercle qui est une réduction de sa base.Son centre appartient à la hauteur du cône.
La section par ce plan parallèle à la base est le cercle de centre I et de rayon IJ.
Le cône de sommet S et de rayon [IJ] est une réduction du cône de sommet S et de rayon [OA].
Rapport de réduction :
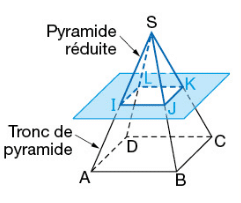
La section d’un pyramide par un plan parallèle à sa base est une réduction de la base.Ses côtés sont parallèles à ceux de la base.
La section par ce plan parallèle à la base carrée est le carré IJKL.
La pyramide de sommet S et de base IJKL est une réduction de la pyramide de sommet S et de base ABCD.
Rapport de réduction :
- Lorsque l’on réduit ou agrandit une figure d’un rapport , alors l’aire de cette figure est multipliée par .
- Lorsque l’on réduit ou agrandit un solide de rapport k, alors son volume est multiplié par .
Exemple :
- Si on agrandit une figure d’un rapport 3, alors son aire sera multipliée par .
- Si on agrandit un solide d’un rapport 2, alors son volume sera multiplié par .
Cette publication est également disponible en :
English (Anglais) 
Español (Espagnol) 
العربية (Arabe)
Télécharger et imprimer ce document en PDF gratuitement
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «sections de solides : cours de maths en 3ème.» au format PDF.
D'autres fiches dans la section cours de maths en 3ème
- Sections planes de solides : cours de maths en 3ème.
- Arithmétique et nombres premiers : cours de maths en 3ème.
- Fonctions affines : cours de maths en 3ème à télécharger en PDF.
- Fonctions linéaires : cours de maths en 3ème.
- Les équations : cours de maths en 3ème en PDF.
- Calcul littéral et les identités remarquables : cours de maths en 3ème
- Sections de solides : cours de maths en 3ème.
- Théorème de Thalès : cours de maths en 3ème en PDF.
- Homothéties : cours de maths en 3ème.
- Probabilités : cours de maths en 3ème.
- 59
Un cours de maths en 3ème sur les volumes de solides et les sections de solides dans l'espace. Nous aborderons dans cette leçon différents rappels sur les aires de figures (rectangle, parallélogramme, trapèze) puis les formules de calculs du volume d'une pyramide, d'un cylindre de révolution ou encore, d'une boule.…
Les dernières fiches mises à jour.
Voici les dernières ressources similaires à sections de solides : cours de maths en 3ème. mis à jour sur Mathovore (des cours, exercices, des contrôles et autres), rédigées par notre équipe d'enseignants.
