Sommaire de cette fiche
- 1 I. La notation scientifique d’un nombre
- 2 II. Les nombres décimaux (purs).
- 3 III.LES NOMBRES RATIONNELS
- 4 IV.LES NOMBRES REELS
- 5 V.La Troncature
- 6 VI. L’arrondi.
- 7 VII. Valeur approchée à l’unité
- 8 VIII.Valeur approchée au dixième
- 9 VIII. Arrondi et valeurs approchées
- 10 IX. Dernière comparaison entre arrondi et valeur approchée selon le signe du nombre décimal
- 11 Vous avez assimilé ce cours sur les rappels des notions du collège en 2de?
I. La notation scientifique d’un nombre
Exemple :
12 345 = 1.2345 x
0.0987 = 9.87 x
II. Les nombres décimaux (purs).
L’écriture décimale d’un nombre se compose d’une partie entière et d’une partie décimale séparéespar une virgule (« , »).
Exemple :
1,5 sa partie entière vaut 1 et sa partie décimale vaut 5
3,14 Sa partie entière vaut 3 et sa partie décimale vaut 14
Règle des 0 non significatifs avant de regarder la partie entière et la partie décimale d’un nombre
A noter qu’on préfère retirer tous les 0 non significatifs(= inutiles) qui précèdent l’écriture d’un nombre, à gauche, et tous les 0 non significatifs qui terminent le nombre à droite.
Exemples:
à gauche des 0 inutiles
001234,56789 s’écrira de préférence 1234,456789 mais par contre peut s’écrire 1234,5678900
à droite des 0 inutiles
10,00 s’écrira de préférence 10 mais peut s’écrire 10,000000
III.LES NOMBRES RATIONNELS
Que dire des nombre qui sont le rapport de deux entiers et de leur écriture décimale?3/2 = 1,5 et c’est simple
Mais .
Pour certains nombres il nous est donc impossible de décrire entièrement leur partie décimale.
IV.LES NOMBRES REELS
Que penser cette fois ci de l’écriture du nombre qui n’est pas égale à 3,14159265 ?
On s’approche avec une certaine précision de sa valeur réelle, mais il nous est impossible d’écrire entièrement sa partie décimale.
On dit qu’on l’a soit tronqué, soit arrondi…avec une certaine précision!
Pour pouvoir écrire, du moins en partie, ces nombres on utilise ce que l’on appelle une troncature ou un arrondi ou encore une valeur approchée.
Par la suite on appellera « nombre décimal » tout nombre (qu’il soit réel, rationnel ou décimal pur) écris avec un nombre fini de chiffres après la virgule.
V.La Troncature
La troncature à l’unité d’un nombre décimal positif est sa partie entière.
On peut l’obtenir en supprimant tous les chiffres à la droite de la virgule.
Exemple :
La troncature à l’unité de 12,637 est 12
On définit aussi, si on veut plus de précision :
-La troncature au dixième:
Exemple:
La troncature au dixième de 12,637 est 12,6
-La troncature au centième, etc.:
Exemples:
La troncature au centième de 12,637 est 12,63
La troncature au millième de 12,637 est 12,637 lui-même
VI. L’arrondi.
L’arrondi à l’unité d’un nombre décimal est le nombre entier le plus proche de celui-ci.
Exemple :
– L’arrondi à l’unité du nombre 56,8 est le nombre entier 57
Par convention, l’arrondi à l’unité du nombre 53,5 est 54
Pour des nombres positifs :
Si le chiffre après la virgule est inférieur à 5 (c’est à dire appartient à {0;1;2;3;4}),
on arrondit à l’entier inférieur.
Exemple :
L’arrondi à l’unité de 53,4 est 53.
Si le chiffre après la virgule est supérieur ou égal à 5 (c’est à dire appartient à {5;6;7;8;9}),
on arrondit à l’entier supérieur.
VII. Valeur approchée à l’unité
- La valeur approchée à l’unité par défaut d’un nombre décimal est le nombre décimal n’ayant pas de virgule. C’est la troncature à l’unité de ce nombre.
- La valeur approchée à l’unité par excès d’un nombre décimal est le nombre sans virgule immédiatement supérieur à ce nombre décimal.
Exemple :
, où 34 est la valeur approchée à l’unité par défaut et 35 la valeur approchée à l’unité par excès.
VIII.Valeur approchée au dixième
Il en ira de même pour « au centième », « au millième », etc.
– La valeur approchée au dixième par défaut d’un nombre décimal est le nombre décimal ayant un seul chiffre après la virgule immédiatement inférieur à ce nombre.
C’est la troncature au dixième de ce nombre.
– La valeur approchée au dixième par excès d’un nombre décimal est le nombre décimal ayant un seul chiffre après la virgule immédiatement supérieur à ce nombre.
Exemples :
à gauche la valeur approchée au dixième par défaut, …
à droite la valeur approchée au centième par excès, à gauche… par défaut
VIII. Arrondi et valeurs approchées
Remarque :
L’arrondi à l’unité, au dixième, au centième d’un nombre décimal est celle des deux valeurs approchées par défaut ou par excès à l’unité, au dixième, au centième, qui est la plus proche de ce nombre.
Exemples :
L’arrondi au dixième de 17,527 est 17,5.
C’est la valeur approchée au dixième par défaut de 17,527.
L’arrondi au dixième de 17,493 est 17,5.
C’est la valeur approchée au dixième par excès de 17,493.
IX. Dernière comparaison entre arrondi et valeur approchée selon le signe du nombre décimal
- L’arrondi de x à l’unité est une valeur approchée de x à 1 près ;si x est positif, cette valeur approchée est par défaut lorsque la première décimale de x est 0, 1, 2, 3 ou 4, par excès lorsque cette décimale est 5, 6, 7, 8 ou 9 ;
- si x est négatif, cette valeur approchée est par excès lorsque la première décimale de x est 0, 1, 2, 3 ou 4, par défaut lorsque cette décimale est 5, 6, 7, 8 ou 9.
- L’arrondi de x au dixième est une valeur approchée de x à 0,1 près ;
- si x est positif, cette valeur approchée est par défaut lorsque la deuxième décimale de x est 0, 1, 2, 3 ou 4, par excès lorsque cette décimale est 5, 6, 7, 8 ou 9 ;
- si x est négatif, cette valeur approchée est par excès lorsque la deuxième décimale de x est 0, 1, 2, 3 ou 4, par défaut lorsque cette décimale est 5, 6, 7, 8 ou 9.
Vous avez assimilé ce cours sur les rappels des notions du collège en 2de?
Effectuez ce QCM sur les rappels des notions à connaître du collège en classe de seconde.
Résumé-Quiz
0 questions correctes sur 12
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
Information
Un QCM sur les nombres relatifs, les fractions et les puissances.
Vous avez déjà rempli le questionnaire avant. Par conséquent, vous ne pouvez pas recommencer.
Quiz is loading...
You must sign in or sign up to start the quiz.
Vous devez finir le quiz suivant, avant de commencer celui-ci :
Résultats
0 questions sur 12 répondues correctement
Votre temps:
Temps écoulé
Vous avez atteint 0 points sur 0 , (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- Répondu
- Examiner
-
Question 1 sur 12
Quelle espression est égale à (+9) – (-15)+(-6)
Exact
Inexact
-
Question 2 sur 12
Quel produit est égal à – 24 ?
Exact
Inexact
-
Question 3 sur 12
Un produit de 5 facteurs est positif.
Combien peut-il y avoir de facteurs négatifs ?
Exact
Inexact
-
Question 4 sur 12
Quel est le résultat de
?
Exact
Inexact
-
Question 5 sur 12
L’expression
est égale à
Exact
Inexact
-
Question 6 sur 12
Quel est le résultat de
?
Exact
Inexact
-
Question 7 sur 12
L’expression
est égale à
Exact
Inexact
-
Question 8 sur 12
L’expression
est égale à
Exact
Inexact
-
Question 9 sur 12
Le nombre
est égal à
Exact
Inexact
-
Question 10 sur 12
L’expression
est égale à
Exact
Inexact
-
Question 11 sur 12
Quelle est la notation scientifique de
?
Exact
Inexact
-
Question 12 sur 12
Quelle est l’écriture décimale du nombre
?
Exact
Inexact
Effectuez un autre QCM sur les opérations et calculs du collège.
Résumé-Quiz
0 questions correctes sur 10
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Un QCM sur les nombres et calculs
Vous avez déjà rempli le questionnaire avant. Par conséquent, vous ne pouvez pas recommencer.
Quiz is loading...
You must sign in or sign up to start the quiz.
Vous devez finir le quiz suivant, avant de commencer celui-ci :
Résultats
0 questions sur 10 répondues correctement
Votre temps:
Temps écoulé
Vous avez atteint 0 points sur 0 , (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Répondu
- Examiner
-
Question 1 sur 10
25-5×3 est égal à
Exact
Inexact
-
Question 2 sur 10
12 : 2 x 3 est égal à
Exact
Inexact
-
Question 3 sur 10
est égal à
Exact
Inexact
-
Question 4 sur 10
se calcule en effectuant
Exact
Inexact
-
Question 5 sur 10
est égal à
Exact
Inexact
-
Question 6 sur 10
est égal à
Exact
Inexact
-
Question 7 sur 10
est égal à
Exact
Inexact
-
Question 8 sur 10
est égal à
Exact
Inexact
-
Question 9 sur 10
L’écriture scientifique de 720 000 000 est
Exact
Inexact
-
Question 10 sur 10
L’écriture scientifique de 0,000 084 est
Exact
Inexact
Un QCM sur les rappels de certaines notions du collège.
Résumé-Quiz
0 questions correctes sur 10
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Un QCM sur les notions d’algèbre abordées au collège.
Vous avez déjà rempli le questionnaire avant. Par conséquent, vous ne pouvez pas recommencer.
Quiz is loading...
You must sign in or sign up to start the quiz.
Vous devez finir le quiz suivant, avant de commencer celui-ci :
Résultats
0 questions sur 10 répondues correctement
Votre temps:
Temps écoulé
Vous avez atteint 0 points sur 0 , (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Répondu
- Examiner
-
Question 1 sur 10
Donner la partie entière de ce nombre décimal (avec des espaces pour faciliter sa lecture):
18967543,65- (18 967 543)
-
Question 2 sur 10
Lequel de ces nombres n’est pas un nombre rationnel simplifié ?
-
Question 3 sur 10
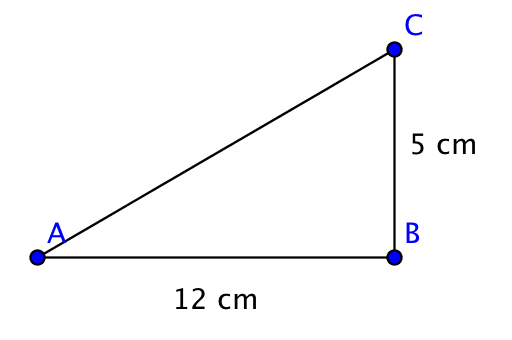
Quelle est la longueur de l’hypoténuse du triangle ci-dessous :
- (13)
-
Question 4 sur 10
Laquelle de ces égalités est correcte ?
-
Question 5 sur 10
Quel est la forme réduite de cette identité remarquable :
-
Question 6 sur 10
Quels choix représentent une inéquation ?
-
Question 7 sur 10
Parmi les égalités suivantes, lesquelles sont justes ?
-
Question 8 sur 10
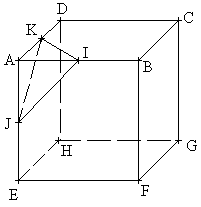
Sachant que ABCDEFGH est un cube d’arête de 12cm, que I, J et K sont respectivement au milieu des segments [AB], [AE] et [AD], quelle est la surface du triangle AKI ?
- (18)
-
Question 9 sur 10
Quelle est la probabilité de ne pas obtenir 3 lors d’un lancé de dé ?
- (5/6)
-
Question 10 sur 10
Quelle est la moyenne des notes des élèves réparties dans le tableau ci-dessous ?
Utiliser . pour la virgule.
- (6,6)




 Mathovore c'est 13 931 280 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 931 280 cours et exercices de maths téléchargés en PDF.