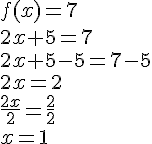Notion de fonction : cours de maths en 3ème à télécharger en PDF.

Les mathématiques sont considérées comme la matière où les élèves rencontrent le plus de difficultés. Mathovore vous permet de travailler sur notion de fonction : cours de maths en 3ème et réviser en ligne par le biais de milliers de ressources rédigées par une équipe d'enseignants volontaires de l'éducation nationale. Vous développerez vos connaissances autant dans le domaine de l'algébre qu'en géométrie. Les mêmes ressources que vous trouverez dans votre manuel scolaire avec des cours complets conformes aux programmes officiels de l'éducation nationale et des exercices corrigés poortant sur chaque chapitre du programme de votre niveau. Chaque document dispose, en bas de page, d'un lien vous permettant de l'exporter au format PDF. Oubliez les cours particuliers qui peuvent être très cher sur une année scolaire. Nos resssources, cours et exercices corrigés sur notion de fonction : cours de maths en 3ème vous permettent de vous exercer en ligne afin de combler vos lacunes en maths et d'envisager une constante progression tout au long de l'année scolaire en développant de nouvelles compétences et en comblant les différentes lacunes que vous rencontrez sur les cours de maths en 3ème . De nombreuses ressources en ligne pour les élèves de primaire (CE2, CM1 et CM1), du collège (6ème, 5ème, 4ème et 3ème) et du lycée (2de, 1ère et terminale) ainsi que de nombreux sujets du brevet des collèges et du baccalauréat afin de vous préparer dans les meileurs conditions pour ces diplômes. Les membres du site ont accès gratuitement aux différents corrigés afin de pouvoir relever les différents erreurs commises sur notion de fonction : cours de maths en 3ème et d'assimiler les différentes notions comme les définitions, les propriétés et les théorèmes.

Sommaire de cette fiche

1 I. Notion de fonction : première approche.
- 1.1 1.Activité d’introduction :
2 II .Vocabulaire et notations sur la notion de fonction :
- 2.1 1. Définition d’une fonction :
- 2.2 2. Notations d’une fonction numérique :
3 III. Courbe représentative d’une fonction :

Les généralités et la notion de fonction numérique dans un cours de maths en 3ème où nous aborderons la notion de fonction avec la définition de l’image et de l’antécédent ainsi que le tableau de valeurs et la courbe représentative d’une fonction dans cette leçon en troisième.

I. Notion de fonction : première approche.

1.Activité d’introduction :

On considère le rectangle MNOP, la longueur x, exprimée en cm, désigne un nombre compris entre 4 et 10.

1. Calculer l’aire du rectangle pour x=4.
L’aire du rectangle est $A_{MNOP}=(4-4)(10-4)=0\times \,6=0\,cm^2$ .

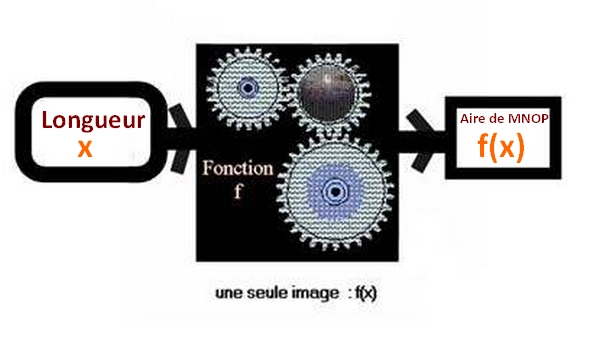
On met en place un procédé mathématiques qui à tout nombre x associe l’aire du rectangle MNOP.

On considère l’aire du rectangle MNOP que l’on note f(x) .

2. Exprimer f(x) à l’aide de la variable x.

$f(x)=Aire_{MNOP}=Longueur\times \,largeur=(10-x)(x-4)$

${\color{DarkRed}f(x)=-x^2+14x-40\,}$

3. Calculer f(5) qui est l’image de 5 par la fonction f.

$f(5)=-5^2+14\times \,5-40=-25+70-40=5\,cm^2$

4. Calculer l’image de 4 par la fonction f, c’est-à-dire f(4).

$f(4)=-4^2+14\times \,4-40=-16+56-40=0\,cm^2$

5. Interpréter ce résultat.

Lorsque la longueur x vaut 4 cm, l’aire du rectangle MNOP vaut $0\,cm^2$ .

Remarque :

le rectangle MNOP est réduit au segment [MN].

6. compléter le tableau de valeurs suivant :

x	4	5	6	7,5	8,5	9
f(x)	0	5	8	8,75	6,75	5

7. Dans le tableau précédent, on lit f(6)=8.

6 étant un antécédent de 8 par la fonction f.

a. Donner un antécédent de 6,75.

Un antécédent de 6,75 par la fonction f est x = 8,5 cm.

b. Déterminer, d’après le tableau ci-dessus, deux antécédents du nombre 5.

Deux antécédents de 5 par la fonction f sont x = 5 cm et x = 9 cm.

c. Pour quelles valeurs de x l’aire du rectangle MNOP vaut-elle 5 ?

D’après la question 3.b., l’aire du rectangle MNOP vaut 5 cm² lorsque x vaut 5 cm ou x vaut 9 cm.

II .Vocabulaire et notations sur la notion de fonction :

1. Définition d’une fonction :

Définition :

Une fonction f est un processus mathématiques qui à tout nombre x associe un unique nombre, noté f(x).
Le nombre f(x) est appelé l’image du nombre x par la fonction f.
Le nombre x est appelé l’antécédent du nombre f(x) par la fonction f.

2. Notations d’une fonction numérique :

Définition :

Il existe deux façons de noter une fonction :

– Soit f la fonction définie par f(x)= 3x+7 .

– ou $f:x\,\mapsto \,3x+7$ se lit la fonction f qui à tout nombre x associe le nombre 3x+7.

Exemple :

Considérons le programme de calcul suivant :

– choisir un nombre x

– Multiplier le résultat par 2

– Ajouter 5

Soit la fonction f qui au nombre x choisi au départ associe le nombre f(x) obtenu à la fin du programme de calcul.

Nous obtenons la fonction f définie par f(x)= 2x+5 .

Calculons l’image de – 3 par cette fonction f :

– 3 est donc un antécédent donc une valeur de x.

Remplaçons x par – 3 dans l’expression de f pour calculer cette image.

$f(-3)=2\times \,(-3)+5=-6+5=-1$

donc l’image de – 3 par cette fonction f est – 1 et réciproquement, – 3 est un antécédent de – 1 par cette fonction f.

Calculons un antécédent de 7 par cette fonction f :

7 est donc une image, on cherche un antécédent de 7, c’est à dire que l’on cherche un nombre x tel que f(x)= 7.

Nous sommes amenés à résoudre l’équation suivante :

$f(x)=7\\2x+5=7\\2x+5-5=7-5\\2x=2\\\frac{2x}{2}=\frac{2}{2}\\x=1$

donc un antécédent de 7 par la fonction f est 1.

Nous pouvons le vérifier en calculant l’image de 1, on doit retrouver 7.

${\color{DarkRed}\,f(1)=2\times \,1+5=2+5=7}$

III. Courbe représentative d’une fonction :

1. Définition de la courbe d’une fonction :

Définition :

Soit f une fonction telle que $f:x\,\mapsto \,f(x)$ .

Soit a un nombre relatif et f(a) son image par la fonction f.

Dans un repère orthonormé, on considère les points M de coordonnées M (a;f(a)) .

L’ensemble de ces points constitue la représentation graphique ( ou courbe représentative) de la fonction f dans ce repère.

Exemple :

Reprenons l’activité du début du cours et la fonction f qui a la longueur x associe l’aire du rectangle MNOP.

Nous avions obtenu l’expression de la fonction f qui est ${\color{DarkRed}f(x)=-x^2+14x-40\,}$ .

2. Tableau de valeurs :

A l’aide d’un tableur, complétons le tableau de valeurs suivant afin de tracer la courbe représentative de cette fonction f.

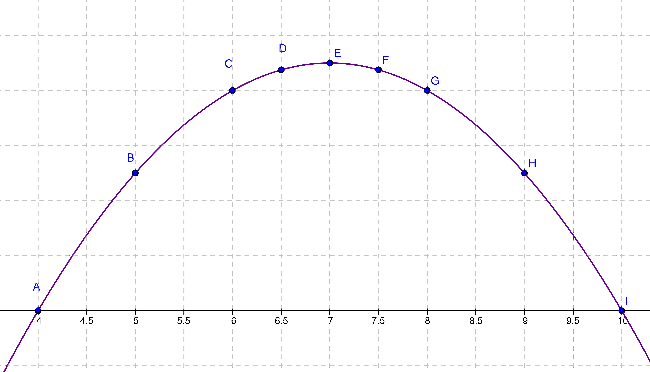
Voici ce que donne la courbe de la fonction f :

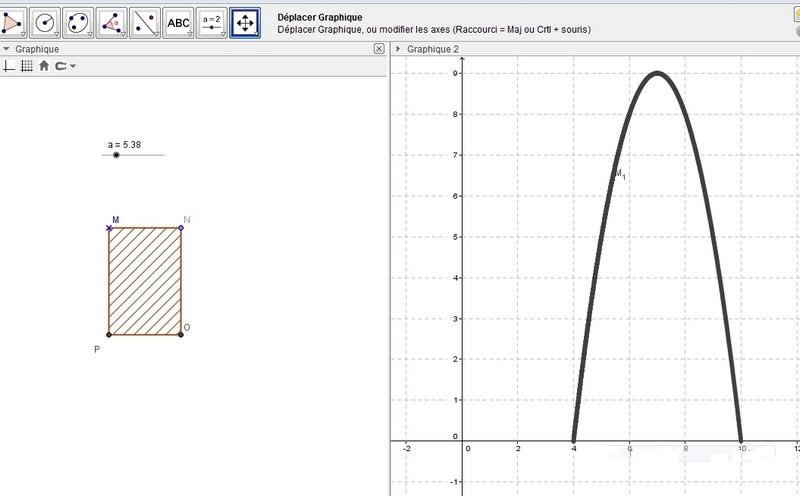
A l’aide du logiciel de géométrie dynamique GEOGEBRA, nous pouvons créer le rectangle MNOP et faire varier la valeur de x entre 4 et 10 et faire afficher dans une seconde fenêtre la courbe de la fonction f, voilà ce que cela donne :

3. Déterminer graphiquement une image ou un antécédent

a. Déterminer une image à l’aide de la courbe de la fonction f

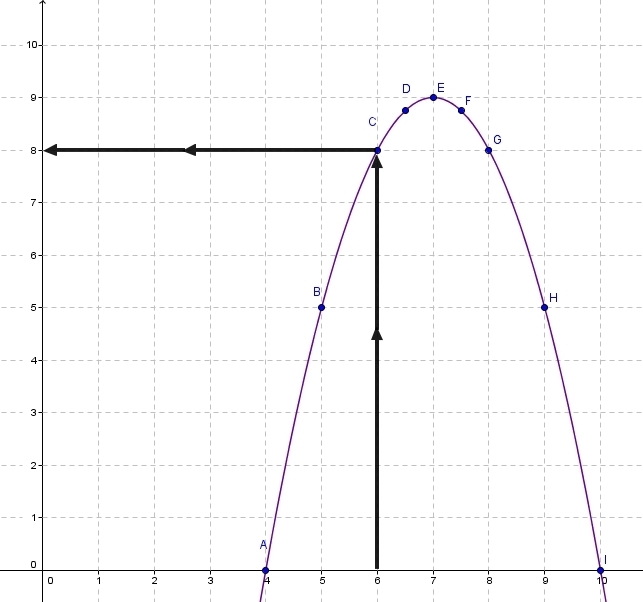
Déterminer l’image de 6 par la fonction f.

L’image de 6 par la fonction f est 8 ce qui équivaut à écrire f(6)=8.

En pratique, cela signifie que lorsque x vaut 6 cm alors l’aire du rectangle MNOP est de 8 cm².

b. Déterminer un antécédent à l’aide de la courbe de la fonction f

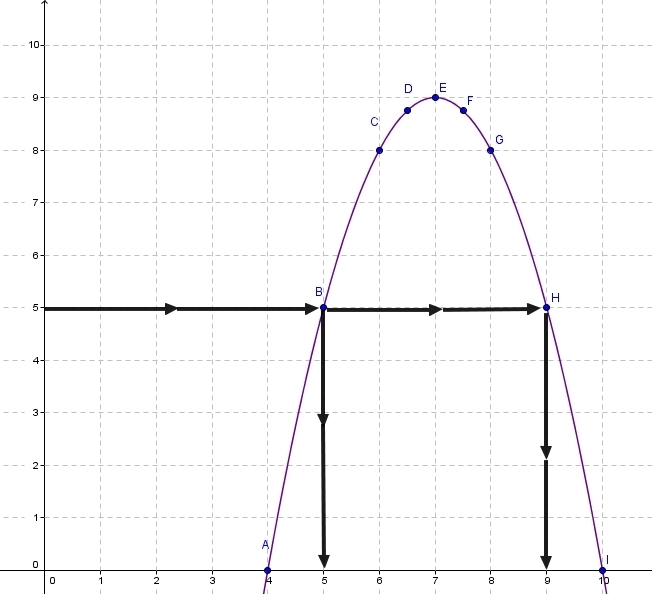
Déterminer le(s) antécédent(s) de 5 par la fonction f.

Il existent deux antécédents de 5 par la fonction f qui sont 5 et 9 ce qui équivaut à écrire que f(5)=5 et que f(9)=5.

En pratique cela signifie que l’aire du rectangle vaut 5 cm² lorsque x vaut 5 cm ou lorsque x vaut 9 cm.

4.2/5 - (8 votes)

Télécharger et imprimer ce document en PDF gratuitement

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «notion de fonction : cours de maths en 3ème» au format PDF.

Télécharger nos applications gratuites avec tous les cours,exercices corrigés.

D'autres fiches similaires à notion de fonction : cours de maths en 3ème.

Mathovore vous permet de réviser en ligne et de progresser en mathématiques tout au long de l'année scolaire.
De nombreuses ressources destinées aux élèves désireux de combler leurs lacunes en maths et d'envisager une progression constante. Tous les cours en primaire, au collège, au lycée mais également, en maths supérieures et spéciales ainsi qu'en licence sont disponibles sur notre sites web de mathématiques.
Des documents similaires à notion de fonction : cours de maths en 3ème à télécharger ou à imprimer gratuitement en PDF avec tous les cours de maths du collège au lycée et post bac rédigés par des enseignants de l'éducation nationale.
Vérifiez si vous avez acquis le contenu des différentes leçons (définition, propriétés, téhorèmpe) en vous exerçant sur des milliers d'exercices de maths disponibles sur Mathovore et chacun de ces exercices dispose de son corrigé.
En complément des cours et exercices sur le thème notion de fonction : cours de maths en 3ème, les élèves de troisième pourront réviser le brevet de maths en ligne ainsi que pour les élèves de terminale pourront s'exercer sur les sujets corrigé du baccalauréat de maths en ligne.

Les intégrales
68
Extraits du baccalaureat S sur les intégrales : Exercice :(Nouvelle-Caledonie) 1. Déterminer trois réels a,b,c tels que , pour tout : . 2. Soit . a. Calculer . b. Soit f la fonction définie sur par En intégrant par parties, calculer f(X) en fonction de X .…
Problèmes de maths et calculs à résoudre à imprimer en PDF.
66
La série des problèmes ouverts de maths afin de réfléchir sur des exercices complexes avec un travail individuel ou en groupe.Ces exercices développe l'esprit d'initiative et le raisonnement scientifique pour les élèves du collège et du lycée. Une série de problèmes ouverts afin de développer la prise d'initiative et le…
Calcul littéral : correction des exercices en troisième
66
Développer avec les identités remarquables, exercices corrigés de mathématiques en troisième (3ème) sur les identités remarquables. Exercice: Développer en utilisant les identités remarquable : Exercice : On considère les expressions E = x² − 5x + 5 et F = (2x − 7)(x − 2) − (x − 3)² .…
Les équations et inéquations : correction des exercices en troisième
65
Résoudre des équations du premier degré à une inconnue.Exercices corrigés de mathématiques en troisième (3ème). Exercice : Exercice : Déterminer trois nombres entier positifs consécutifs dont la somme des carrés est égale à 1 325. Pour la facilité des calculs on choisira les nombres consécutifs suivants : n-1…
Variations de fonctions et extremums : cours de maths en 2de
63
Un cours sur les variations de fonctions et les extremums en 2de avec la croissance et décroissance d'une fonction ainsi que le tableau de variation. Nous étudierons, dans cette leçon en seconde, l'aspect algébrique puis l'aspect graphique de l'étude des variations d'une fonction. Les connaissances de collège nécessaires pour aborder…

Les dernières fiches mises à jour

Voici les dernières ressources mis à jour sur Mathovore (des cours, exercices, des contrôles et autres), rédigées par notre équipe d'enseignants.

Mathovore c'est 2 493 864 cours et exercices de maths téléchargés en PDF et 184 556 membres.
Rejoignez-nous : inscription gratuite.