La récurrence : exercices de maths en terminale corrigés en PDF.

Le raisonnement par récurrence avec des exercices de maths en terminale corrigés portant sur l’initialisation et l’hérédité d’une propriété que l’on considère vraie au rang n et que l’on démontre qu’elle reste vraie au rang n+1.Ces exercices sont entièrement corrigés avec les réponses qui sont détaillées et les fichiers peuvent être téléchargés gratuitement au format PDF.

Exercice 1

Soit $(U_n) \,$ la suite définie par

$\{{U_0=2\atop \forall n \in\,\mathbb{N}\,\,U_{n+1}=\sqrt{U_n+2}} \,.$

Démontrer par récurrence que :

$\fbox{\forall n \in\,\mathbb{N}\,,\,U_n\le2 }\,$

Exercice 2

Soit $(U_n) \,.$ la suite définie par

$\{{U_0=2\atop \forall n \in\,\mathbb{N}\,,\,U_{n+1}=2U_n-3} \,.$

Démontrer par récurrence que :

$\fbox{\forall n \in\,\mathbb{N}\,,\,U_n=3-2^n }\,.$

Exercice 3

On pose :

$\forall n \in\,\mathbb{N^*}\,,\,S_n=1^2+2^2+3^2+....+n^2=\sum_{k=1}^n k^2 \,.$

a. Calculer $S_1\,S_2\,,S_3\,,S_4 \,.$

b. Exprimer $S_{n+1}$ en fonction de $S_n$ .

c. Démontrer par récurrence que :

$\fbox{ \forall n \in\,\mathbb{N^*}\,\,S_n=\frac{n(n+1)(2n+1)}{6} }\,.$

Exercice 4 – Démonstration avec deux variables

On note $x$ et $y$ deux réels .

1. Démontrer que pour tout $n\in \mathbb{N}$ alors $x^{n+1}-y^{n+1}=y(x^n-y^n)+(x-y)x^n$ .

2. Exprimer $x^ky^{n-k}$ en fonction de $x$ , si k = n .

3. Démontrer par récurrence que pour tout $n\in \mathbb{N}^*$ alors $x^n-y^n=(x-y)\sum_{k=0}^{n-1}x^ky^{n-1-k}$ .

Exercice 5 – Raisonnement et démonstration de propriétés

Démontrer les propriétés ci-dessous :

1. Si $a\in \mathbb{Q}$ et $x\notin \mathbb{Q}$ alors $a+x\notin \mathbb{Q}$ .

2. Si $a\in \mathbb{Q}^*$ et $x\notin \mathbb{Q}$ alors $a\times x\notin \mathbb{Q}$ .

Exercice 6 – Démontrer par récurrence une somme

On note $x$ un réel différent de 1.

Démontrer par récurrence que pour tout $n\in \mathbb{N}$ , $\sum_{k=0}^{n}x^k=\frac{1-x^{n+1}}{1-x}$ .

Exercice 7 – Calcul d’une somme

Démontrer par récurrence que pour tout $n\in \mathbb{N}^*$ ,

on a $\sum_{k=1}^{n}(-1)^kk=\frac{(-1)^n(2n+1)-1}{4}$ .

Exercice 8 – Raisonnement par récurrence et puissance

On note x un réel positif .

Démontrer par récurrence que pour tout entier $n\in \mathbb{N}$ , on a $(1+x)^n\geq\, 1+nx$ .

Exercice 9 – Raisonnement par contraposée

On note $n\in \mathbb{N}^*$ .

Le but de cet exercice est de montrer par contraposée la propriété suivante :

Si l’entier $n^2-1$ n’est pas divisible par 8 alors l’entier n est pair .

1. Ecrire la contraposée de la proposition précédente .

2. En remarquant qu’un entier impair n s’écrit sous la forme $n=4k+r$

avec $k \in \mathbb{N}$ et $r \in \{1,2,3 \}$ ( à justifier).Prouver la contraposée .

3. Que peut-on en déduire ?

Exercice 10 – Somme des cubes

1. Montrer que $\forall n\in \mathbb{N}^*\,,\sum_{k=1}^{n}k^3=\frac{n^2(n+1)^2}{4}$ .

2. En déduire la valeur de $A=1^3+2^3+3^3+4^3+...+10^3$

Multiples

Montrer que, pour tout entier $n\geq\, 0$ , $n^3-n$ est un multiple de 3 .

Exercice 11 – Montrer que c’est un multiple

1. Développer, réduire et ordonner $(n+1)^5$ .

2. En déduire que pour tout entier $n\geq\, 0$ , $n^5-n$ est un multiple de 5 .

Exercice 12 – Démonstration par récurrence

Démontrer par récurrence que, pour tout entier naturel non nul n,on a :

$\sum_{k=1}^{n}k^3= ( \sum_{k=1}^{n} k )^2$ .

Rappel : $\sum_{k=1}^{n}k=\frac{n(n+1)}{2}$

Exercice 13 :

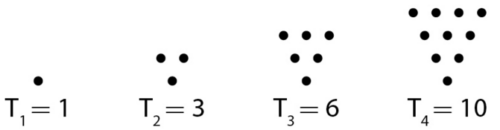
Voici les quatre premiers nombres triangulaires :

1. Représenter $T_5$ et $T_6$ .
2.a) Pour tout entier naturel $n\,\geq\,\,1$ , exprimer $T_{n+1}$ en fonction de $T_n$ .
b) Conjecturer l’expression de $2T_n$ , puis de $T_n$ en fonction de n.
c) Valider cette conjecture par récurrence.

Exercice 14 :

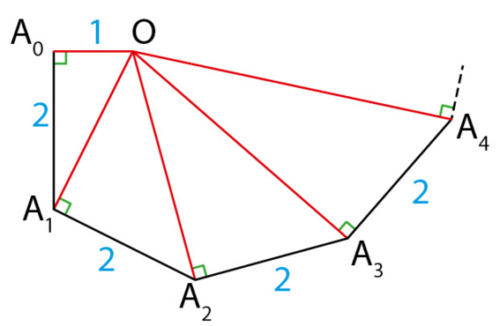
Sur cette figure :

$OA_0=1$
$A_0A_1\,=A_1A_2=...=2;$
les triangles $OA_0A_1$ , $OA_1A_2$ , … sont rectangles.

Démontrer par récurrence que pour tout entier naturel n, $OA_n=\sqrt{4n+1}$ .

Exercice 15 :

Voici deux fonctions écrites en langage Python par des élèves.

a) Décrire les suites $(u_n)$ et $(v_n)$ dont ces fonctions permettent de calculer les termes.
b) Les deux élèves remarquent que les valeurs affichées pour un même entier naturel n saisi sont identiques pour les deux programmes.
Émettre alors une conjecture et la démontrer.

Exercice 16 :

Le programme ci-dessous écrit en langage Python permet de comparer les premiers termes de deux suites $(u_n)$ et $(v_n)$ définies pour tout entier naturel $n\,\geq\,\,1$ .

a) Décrire les deux suites $(u_n)$ et $(v_n)$ .
b) Saisir et exécuter ce programme pour n = 15.
c) Émettre alors une conjecture et la démontrer.
d) Comment expliquer les résultats obtenus pour n = 30 ?

Exercice 17:

$(u_n)$ est la suite définie par $u_0=0$ et pour tout entier naturel n, $u_{n+1}=4+5u_n$ .
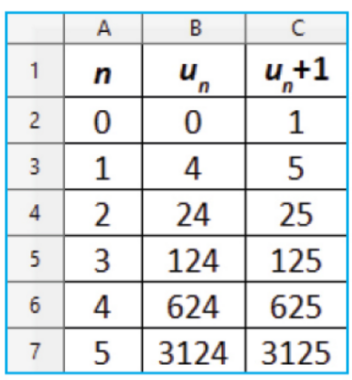
Manon a réalisé la feuille de calcul ci-dessous.

a) Émettre une conjecture sur l’expression de $u_n$ en fonction de n.
b) Démontrer cette conjecture par récurrence.

4.3/5 - (76 votes)

´