Limites et asymptotes : cours de maths en terminale en PDF.

cours de maths en terminale S

Sommaire de cette fiche

1 I.Limite d’une fonction en l’infini
- 1.1 1. Limite finie en l’infini
2 II. Limite infinie en l’infini
- 2.1 2. Limite infinie en un réel
3 III. Opérations sur les limites.
4 IV. Limite d’une fonction composée
- 4.1 1. Fonction composée
- 4.2 2. Théorème de composition des limites
5 V. Limites et comparaison
- 5.1 1. Théorème de comparaison
- 5.2 2. Théorème d’encadrement dit « des gendarmes » ou « sandwich ».

Les limites (somme, produit, quotient) dans un cours de maths en terminale avec l’étude des formes indéterminées. Dans cette leçon, nous mènerons une études des asymptotes horizontales, verticales et obliques en terminale S pour l’enseignement obligatoire.
Connaissances nécessaires à ce chapitre :
$\star\,$ Déterminer la limite éventuelle d’une suite géométrique.
$\star\,$ Étudier la limite d’une somme, d’un produit ou d’un quotient
de deux suites.
$\star\,$ Utiliser un théorème de comparaison ou d’encadrement
pour déterminer une limite de suite.
$\star\,$ Établir (par dérivation ou non) les variations d’une fonction.

I.Limite d’une fonction en l’infini

Dans toute cette partie, désigne la courbe représentative de la fonction f dans un repère quelconque du plan.

1. Limite finie en l’infini

Définition :

Soit f une fonction définie au moins sur un intervalle de $\mathbb{R}$ du type $]a\,;\,+\infty[$ .
La fonction f a pour limite ℓ en $+\infty$ si tout intervalle ouvert contenant ℓ contient toutes les
valeurs de f (x) pour x assez grand. On note alors : $\lim_{x\to\,+\infty}f\,(x)\,=\,l$ .

Exemple :

Soit f la fonction définie sur $]0\,;\,+\infty[$ par $f\,(x)\,=\frac{1}{x}+\,1$ . On a $\lim_{x\to\,+\infty}\,(\,\frac{1}{x}+1\,\,)\,=\,1$ .
En effet, l’inverse de x se rapproche de 0 à mesure que x augmente.
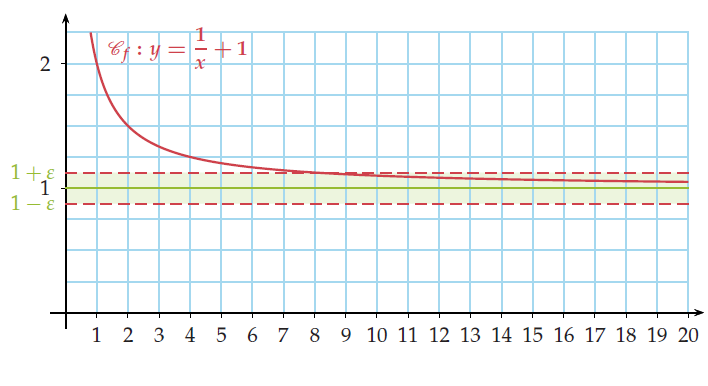
Soit un intervalle ouvert I tel que $1\in\,I$ . Alors, f (x) sera toujours dans I pour x assez grand.
Graphiquement, aussi étroite que soit une bande parallèle à la droite d’équation y = 1 et qui la
contient, il existe toujours une valeur de x au delà de laquelle ne sort plus de cette bande.

Asymptote horizontale.

La droite d’équation y = ℓ est asymptote horizontale à

en $+\infty$ si $\lim_{x\to\,+\infty}f\,(x)\,=\,l$ .

Remarque :

On définit de façon analogue $\lim_{x\to\,-\infty}f\,(x)\,=\,l$ qui caractérise une asymptote horizontale à en $-\infty$ d’équation y = ℓ.

Exemple :

On a vu précédemment que $\lim_{x\to\,+\infty}\,(\,\frac{1}{x}+1\,\,)\,=\,1$ . On a aussi $\lim_{x\to\,-\infty}\,(\,\frac{1}{x}+1\,\,)\,=\,1$ .
Donc, la droite d’équation y = 1 est asymptote horizontale à la courbe en $+\infty$ et en $-\infty$ .

Propriété (admise) : limites finies des fonctions usuelles en ± $\infty$ .

Soit n un entier naturel non nul.
$\lim_{x\to\,+\infty}\frac{1}{\sqrt{x}}=\lim_{x\to\,+\infty}\frac{1}{x^n}=0$

et $\lim_{x\to\,-\infty}\frac{1}{x^n}=0$

II. Limite infinie en l’infini

Définition :

La fonction f a pour limite $+\infty$ en $+\infty$ si tout intervalle de $\mathbb{R}$ du type $]a\,;\,+\infty[$ contient
toutes les valeurs de f (x) pour x assez grand. On note alors : $\lim_{x\to\,+\infty}f\,(x)\,=\,+\infty$

Exemple :

Soit f la fonction racine carrée. On a $\lim_{x\to\,+\infty}\,\sqrt{x}\,=\,+\infty$ .
En effet, $\sqrt{x}$ devient aussi grand que l’on veut à mesure que x augmente.
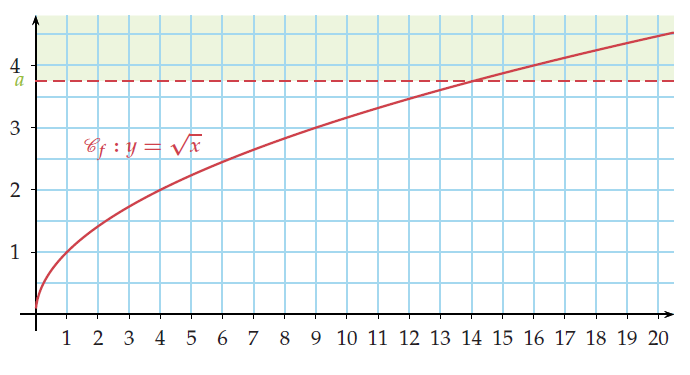
Soit un intervalle ouvert $I\,=]a\,;\,+\infty[$ . Alors, f (x) sera toujours dans I pour x assez grand.
Graphiquement, si on considère le demi-plan supérieur de frontière une droite d’équation
y = a, il existe toujours une valeur de a au-delà de laquelle ne sort plus de ce demi-plan.

Propriété (admise) : limites infinies des fonctions usuelles en ± $\infty$ .

Soit n un entier naturel non nul.
$\lim_{x\to\,+\infty}\sqrt{x}=\lim_{x\to\,+\infty}x^n=+\infty$

et $\lim_{x\to\,-\infty}x^n=0\,(+\infty\,\,si\,\,n\,pair\,;\,-\infty\,si\,\,n\,impair\,).$

2. Limite infinie en un réel

Définition :

Soit f une fonction définie sur un intervalle ouvert de $\mathbb{R}$ du type $]x_0\,-\varepsilon\,;\,x_0[$ ou $]x_0\,;\,x_0+\varepsilon[$ .
La fonction f a pour limite $+\infty$ en

si tout intervalle de $\mathbb{R}$ du type $]A\,;\,+\infty[$ contient toutes
les valeurs de f (x) pour x assez proche de

. On note alors : $\lim_{x\to\,x_0}f\,(x)\,=\,+\infty$

Définition : asymptote verticale.

La droite d’équation

est asymptote verticale à

si $\lim_{x\to\,x_0}f\,(x)\,=\,+\infty$

ou $\lim_{x\to\,x_0}f\,(x)\,=\,-\infty$

Propriété (admise) : limites finies des fonctions usuelles en 0.

Soit n un entier naturel non nul.
$\lim_{x\to\,0^+}\frac{1}{\sqrt{x}}=\lim_{x\to\,0^+}\frac{1}{x^n}=+\infty$

et $\lim_{x\to\,0^+}\frac{1}{x^n}=0\,(+\infty\,\,si\,\,n\,pair\,;\,-\infty\,si\,\,n\,impair\,).$

III. Opérations sur les limites.

Propriété : limite d’une somme, d’un produit et d’un quotient de deux fonctions.

IV. Limite d’une fonction composée

1. Fonction composée

Définition :

Soit f une fonction définie sur E et à valeurs dans F, et soit g une fonction définie sur F.
La composée de f suivie de g est la fonction notée $g\,o\,f$ définie sur E par $g\,o\,f\,(x)\,=\,g(\,f\,(x))$ .

Remarque :

Il ne faut pas confondre $g\,o\,f$ et $fo\,g$ qui sont, en général, différentes.

2. Théorème de composition des limites

Théorème :

Soit h la composée de la fonction f suivie de g et a, b et c trois réels ou ± $\infty$ .
Si $\lim_{x\to\,a}f\,(x)\,=\,b$ et $\lim_{x\to\,b}g\,(x)\,=\,c$ , alors $\lim_{x\to\,a}h\,(x)\,=\,c$ .

V. Limites et comparaison

1. Théorème de comparaison

Théorème :

2. Théorème d’encadrement dit « des gendarmes » ou « sandwich ».

Théorème :

Soit deux réels a et ℓ et trois fonctions f , g et h telles que, pour x > a, on a $f\,(x)\,\leq\,\,g(x)\,\leq\,\,h(x)$

.
Si $\lim_{x\to\,+\infty}f\,(x)\,=\lim_{x\to\,+\infty}h\,(x)\,=\,l$

, alors $\lim_{x\to\,+\infty}g\,(x)\,=l$ .

Remarque :

On a, comme pour le théorème de comparaison précédent, deux théorèmes
analogues lorsque x tend vers − $\infty$ et lorsque x tend vers un réel .

Exemple :

Déterminons la limite en − $\infty$ de $f\,(x)\,=\,\frac{x\,cos\,x\,}{x^2\,+\,1}$ .
La limite de cos x en − $\infty$ est indéterminée. Donc celle de f (x) aussi.
Cependant pour tout x réel strictement négatif, $-1\,\leq\,\,cos\,x\,\leq\,\,1$ donc $x\,\leq\,\,x\,cos\,x\,\leq\,\,-x$ .
Et en divisant membre à membre par $x^2\,+\,1\,>\,0$ on a :
$\frac{x}{x^2+1}\leq\,\,\frac{x\,cos\,x}{x^2+1}\leq\,\,\frac{-x}{x^2+1}$ .

Pour $x\,\in\,R\,^*$ , $\frac{x}{x^2\,+\,1}=\frac{1}{x+\frac{1}{x}}$ .

Or, $\lim_{x\to\,-\infty}x+\frac{1}{x}=-\infty$ donc $\lim_{x\to\,-\infty}\frac{x}{x^2\,+\,1}=\lim_{x\to\,-\infty}\frac{-x}{x^2\,+\,1}=0$

Donc, d’après le théorème des gendarmes, $\lim_{x\to\,-\infty}\frac{x\,cos\,x\,}{x^2\,+\,1}=0$ .

Cette publication est également disponible en : English (Anglais) Español (Espagnol) العربية (Arabe)

Télécharger et imprimer ce document en PDF gratuitement

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «les limites et les asymptotes : cours de maths en terminale.» au format PDF.

D'autres fiches dans la section cours de maths en terminale S

Télécharger nos applications gratuites avec tous les cours et exercices corrigés.

D'autres fiches similaires à les limites et les asymptotes : cours de maths en terminale..

Fonction continue : cours de maths en terminale en PDF.
87
La continuité d'une fonction numérique dans un cours de maths faisant intervenir le théorème des valeurs intermédiaires. Nous terminerons cette leçon par l'interprétation graphique et les propriétés de la continuité. Remarque : Les programmes limitent la continuité à une approche intuitive qui est de considérer qu’une fonction est continue sur un…
La fonction exponentielle : cours de maths en terminale en PDF.
87
La fonction exponentielle avec un cours de maths en terminale où nous étudierons une première approche à l'aide des équations différentielles. Puis nous verrons les différentes propriétés, les définitions et limites usuelles de la fonction exponentielle et la courbe représentative de la fonction. I . Equation différentielle f ’ =…
Cours de maths en terminale à télécharger en PDF.
83
Des cours de maths en terminale que vous pouvez télécharger en PDF gratuitement puis les imprimer sur les très nombreux chapitres de ce niveau qui représente la dernière étape du lycée qui se conclue par les épreuves du baccalauréat durant 4 heures. Les leçons parcourent tous les chapitres comme les nombres,…

Les dernières fiches mises à jour.

Voici les dernières ressources similaires à les limites et les asymptotes : cours de maths en terminale. mis à jour sur Mathovore (des cours, exercices, des contrôles et autres), rédigées par notre équipe d'enseignants.

Mathovore c'est 13 624 718 cours et exercices de maths téléchargés en PDF.