Sommaire de cette fiche
Les fonctions affines dans un cours de maths en 3ème où nous aborderons la définition et le calcul d’image ou d’antécédent puis nous verrons la représentation graphique ou la courbe d’une fonction. Dans cette leçon en troisième, nous déterminerons l’expression algébrique d’une fonction affine connaissant deux points de sa courbe.
Dans cette leçon, nous considérerons comme acquis le chapitre sur les fonctions linéaires .
On se placera dans un repère .
I. Les fonctions affines :
1.Activité d‘introduction :
Considérons un rectangle de longueur x cm et de largeur 3 cm.
Notons y son périmètre.
Nous allons étudier les variations du périmètre en fonction de celles de la longueur.
a. Compléter le tableau de valeur suivant :
| Longueur (en cm) | 1 | 2 | 4 | 5 |
| Périmètre (en cm) | 8 | 10 | 14 | 16 |
b. Ce tableau représente-t-il une situation de proportionnalité ?
c. Le périmètre est-il une fonction linéaire de la longueur du rectangle ?
d. Donner une relation (égalité) reliant y et x.
On dit que le périmètre (y) est une « fonction affine » de la longueur (x).
Nous avons d‘après la formule du périmètre d‘un rectangle
e. Dans le repère (O, , placer les points A(1,8) B(2 ;10) C(4 ;14) D(5 ;16).
f. Quelles sont vos remarques ?
Tous les points sont alignés sur une droite.
2. Définition :
Soient a et b deux nombres relatifs donnés.
La fonction affine f de coefficients a et b est définie par la relation :
A tout nombre x on associe le nombre.
On note ( où f définie par
)
Le nombre f(x) est appelé image de x par la fonction f.
Exemples :
Dans l‘activité précédente la périmètre est une fonction affine f de la longueur.
En notant x la longueur. O
n a f(x)= 2x+6 avec a=2 et b=6.
Si a = 3 et b = -5 alors la fonction affine est : .
Calculer l‘image des nombres 2 et -3 par f.
donc l‘image de 2 par f est 1.
Remarque :
Une fonction linéaire est une fonction affine puisqu’elle s‘écrit avec b=0.
La réciproque est fausse.
Une fonction affine n‘est pas toujours linéaire.
Contre-exemple : est affine mais pas linéaire.
3. Courbe représentative d‘une fonction affine :
Dans l‘activité d‘introduction, nous avons remarqué que la courbe est une droite,
Cette propriété est généralisée pour toutes les fonctions affines.
La représentation graphique d‘une fonction affine est une droite.
Cette droite a pour équation réduite y=ax+b.
a est appelé « le coefficient directeur »
et b « l‘ordonnée à l‘origine ».
Remarque :
b s‘appelle l‘ordonnée à l‘origine car f(0)=ax0+b=b donc la droite passe par le point de coordonnées (0,b) donc par l‘ordonnée à l‘origine.
Exemple :
Représenter graphiquement .
Méthode :
Le principe est le même que pour les fonctions linéaires.
Sauf que dans ce cas il nous faut deux points.
Prenons deux valeurs de x différentes et calculons leur image.
| Valeur de x | 0 | 2 |
Valeur de f(x) |
2 | 8 |
| Points de la droite | A(0;2) | B(2;8) |
II.Détermination de l‘expression d‘une fonction affine par le calcul :
Méthode :
Le procédé est similaire à celui des fonctions affines sauf que dans ce cas nous avons deux coefficients (a et b) déterminer donc il nous faut deux informations donc les coordonnées de deux points.
Exemple :
Déterminer l‘expression de la fonction f dont la courbe passe par les points A(2,5) et B (-1 ;-1)
y= ax+b
A appartient à la droite donc ses coordonnées vérifient l‘équation 5=2a+b.
B appartient à la droite donc ses coordonnées vérifient l‘équation -1=-1a+b.
Nous sommes donc amenés à résoudre le système suivant :
Après résolution, nous obtenons a =2 et b=1.
Conclusion :
La fonction f recherchée est : .
Remarque :
b s‘appelle l‘ordonnée à l‘origine car donc la droite passe par le point de coordonnées (0,b) donc par l‘ordonnée à l‘origine.
Si le chapitre sur les systèmes n‘a pas été étudié,
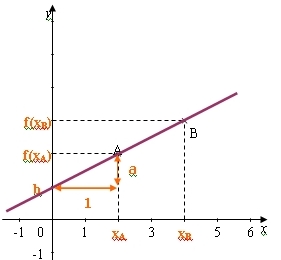
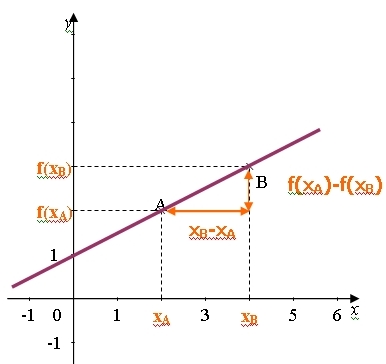
a est le coefficient de proportionnalité entre les accroissements de
f(x) et ceux de x donc pour tout nombres et
distincts
Donc
et b s‘obtient en résolvant ou
.
Retrouvons l‘expression de la fonction f par cette méthode :
ensuite
5=2a+b
5=2×2+b
b=5-4=1
ou
-1=2x(-1)+b
-1=-2+b
b=-1+2=1
Conclusion :
nous retrouvons bien a=2 et b=1 donc .
Vous avez assimilé ce cours sur les fonctions affines en 3ème ?
Effectuez ce QCM sur les fonctions affines en classe de troisième.
Un QCM sur les fonctions affines







 Mathovore c'est 13 927 329 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 927 329 cours et exercices de maths téléchargés en PDF.