Exercice 1 :
Etablir le tableau de signe des expressions algébriques suivantes :
a.
b.
c.
Exercice 2 :
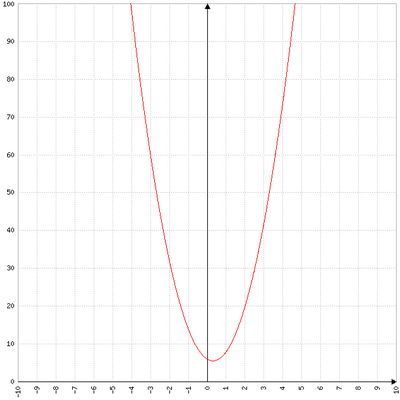
1. Etablir le tableau de signe de l’expression algébrique suivante :
2. Résoudre :
3.
a. Développer .
b. Résoudre :
.
Exercice 3 :
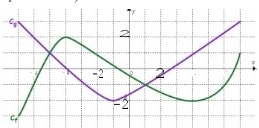
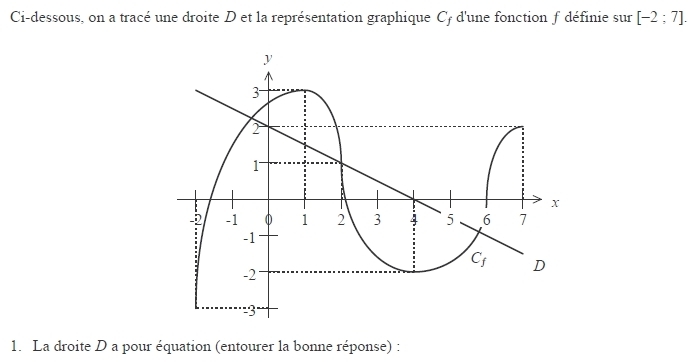
1. Considérons les courbes représentatives des fonctions f et g suivantes :
a. Résoudre .
b. Résoudre .
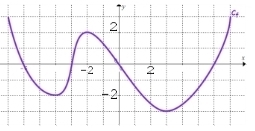
2. Considérons la courbe représentative de la fonction f suivante :
Résoudre les équations et inéquations suivantes :
a. .
b. .
c. .
Exercice 4 :
On considère les fonctions f et g définies par :
.
1. Déterminer l’ensemble de définition de ces deux fonctions.
2. Déterminer l’image de 3 et -1,5 par ces fonctions.
3. Calculer ..
4. Déterminer les antécédents de 4 par ces deux fonctions .
Exercice 5 :
On considère la fonction g définie par :
.
1. Déterminer l’ensemble de définition de la fonction g .
2. Déterminer les antécédents de 2 par la fonction g (donner les résultats sous forme simplifiée).
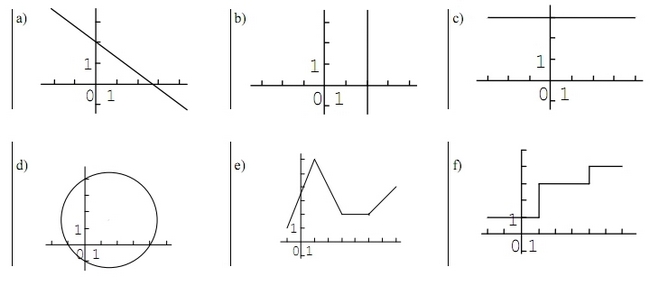
Exercice 6 – Représentation graphique
Pour chacune des courbes ci-dessous, indiquer si c’est la représentation graphique d’une fonction.
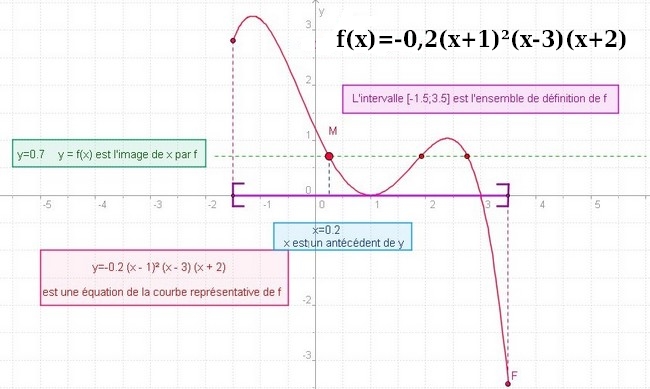
Exercice 7 – Image et antécédent
1. Déterminer par lecture graphique les images de 1et de 2.5 par la fonction f. (à 0.1 près)
2. Retrouver les valeurs exactes de ces résultats par le calcul.
3. Déterminer graphiquement les antécédents de 1. ( toujours à 0.1 près)
4. Résoudre graphiquement l’équation f(x) =0.
5. Résoudre graphiquement l’inéquation f(x)> 1.
Exercice 8 – Fonctions et calcul littéral
On donne
f(x) = 9x² – 4 + (3-2 x) (3x-2) et g (x) = x² +2x +1 – (2x-3)²
1. Développer, réduire et ordonner f(x) et g (x). (1 pt)
2. Factoriser f (x) et g (x).
Soit la fonction rationnelle définie par h(x) = (f(x))/(g(x))
1. Déterminer la condition d’existence de h(x).
2. Simplifier h(x).
3. Résoudre les équations et inéquations suivantes :
h(x) = 0 ; h(x) = 3 et h(x) < 0.
Exercice 9 – Etude d’un rectangle et fonction numériques
et
désignent des réels strictement positifs .
Un rectangle de dimension et
(en centimètres) a pour aire
.
a) Exprimer en fonction de
.
b) On définit une fonction en associant à la dimension ,
l’autre dimension .
Quel est l’ensemble de définition de cette fonction ?
Exercice 10 – Tableau de signe et étude d’une fonction
f est la fonction définie sur par
.
1- Démontrer que, pour tout nombre réel x, .
2- Résoudre graphiquement l’inéquation .
3- Factoriser et retrouver les solutions de l’inéquation à l’aide d’un tableau de signes.
Exercice 11 – Etude d’une fonction numérique
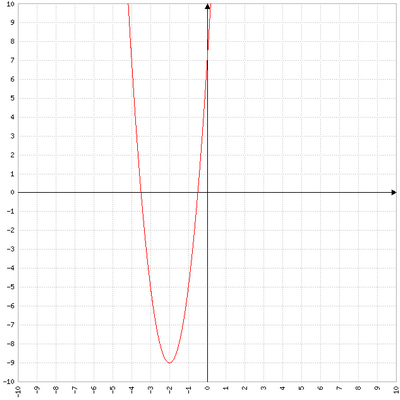
Soit f la fonction définie sur R par f(x) = 4x² + 16x + 7
1) démontrer que f(x) = 4(x+2)²-9
2) factoriser f(x)
3) choisir la forme la mieux adaptée et détailler les calcules pour calculer f(-1/2) et f()
4) Dans le repère suivant tracer la représentation graphique de f
5 ) résoudre algébriquement f(x) = 0. Expliquer comment controler les solutions sur le graphique
6a) résoudre algébriquement l’équation f(x) = 2x+7
b) résoudre graphiquement la même équation
7) quelle forme de f(x) permet d’affirmer que f(x) est toujours supérieur ou égal a -9.
Démontrer alors que pour tout x de R, f(x) est toujours supérieur ou égal a -9.
Comment contrôler ce résultat sur le graphique ?
Exercice 12 – Exercices sur les fonctions
1. On considère les fonctions f, g , h définies sur par :
.
a. Donner l’expression algébrique de la fonction composée i=hofog .
b. Calculer l’image de -1;0 et 1 par la fonction i .
c. Calculer les antécédents de 27 par i.
2. Décomposer les fonctions suivantes à l’aide des fonctions de référence (fonctions usuelles).
a. .
b. .
c. .
d. .
Exercice 13 :
On considère la fonction f définie sur par :
.
1. Montrer l’égalité des expressions algébriques suivantes :
2. On considère, désormais, la fonction f définie par :
a. f=hokom avec
b. Déterminer le sens de variation de la fonction f sur chacun les intervalles et
.
c. Dresser le tableau de variation de la fonction f sur .
d. En déduire la valeur minimale de f sur , en quel point est-elle atteinte?
e. Retrouver le résultat de la question d. à l’aide de l’expression algébrique de f.
Exercice 14 – Vocabulaire sur les fonctions
Traduire les phrases suivantes à l’aide d’égalités :
a. Par la fonction g, – 5 est l’image de 4.
b. 2 a pour image 0 par la fonction f.
c. Un antécédent de – 3 par h est 5.
d. Les images par f de – 3 et 5 sont nulles.
Exercice 15 – Etude de deux fonctions numériques
Soient f et g deux fonctions définies sur par :
et
.
1. Tracer à l’écran de la calculatrice les courbes représentatives des fonctions
f et g.
2. Conjecturer graphiquement les solutions de l’équation .
3. Résoudre algébriquement l’équation .
4. En déduire les coordonnées des points d’intersection des deux courbes.
Exercice 16 – Développer et réduire l’expression de la fonction
Développer, puis réduire, l’expression de la fonction définie sur
par :
Exercice 17 – Fonctions et géométrie
Soit ABCD un carré de côté 20
Soit M un point de [AB]. On note x la distance AM
Les points P et N sont définis tel que AMNP soit un carré et P appartient à [AD]
Soit f(x) l’aire du carré AMNP et g(x) l’aire du triangle DNC
1. Exprimer f(x) en fonction de x
2. Exprimer g(x) en fonction de x
3.Représenter dans un même repère les fonctions f et g pour tout x de [0;20]
4.Déterminer graphiquement les valeurs de x pour lesquelles le carré AMNP et le triangle DNC ont la même aire
Exercice 18 – Etude d’une fonction
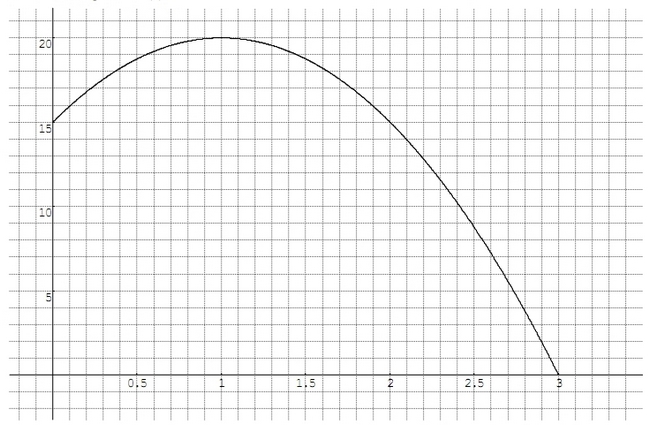
La trajectoire d’une balle de jeu est donné par f(x) = – 5 x² + 10 x + 15 .
où x est le temps écoulé depuis le lancement en l’air, exprimé en secondes, avec x ∈ [0 ; 3],
et f(x) est la hauteur de la balle au dessus du sol, exprimée en mètres .
Partie A. Lecture graphique.
On a représenté graphiquement la fonction f ci-dessous .
Répondre aux questions suivantes en utilisant le graphique.
1° a) Quelle est la hauteur de la balle après 10 secondes ?
b) A quelle hauteur était la balle quand elle a été lancée ?
c) La balle peut-elle être lancée à 20 m ?
d) Au bout de combien de temps est-elle revenue au sol ?
e) Déterminer f(3) et f(0). Que représente ce nombre ?
2° a) Quelle est la hauteur maximale atteinte par la balle
b) Donner les instants où la hauteur est égale à 15 m
c) Résoudre graphiquement f(x) 18. Donner une interprétation concrète de cette inéquation.
Partie B : Calculs .
1° Par le calcul retrouver les résultats de la partie A 1° b) et 1° d
2° a) Démontrer que pour tout réel x de [ 0 ; 3 ], .
b) Résoudre l’équation : f(x) = 15. Quel résultat de la partie A retrouve-t-on ?
3° Démontrer que pour tout réel x de [ 0 ; 3 ], f(x) 20.
Quel résultat de la partie A retrouve-t-on ?
4° calculer et
.
5° Résoudre l’équation : f(x) = 0.
Exercice 19 :
Soit la fonction linéaire .
a. Calculer f(5) ; f(- 1,2) ; f(0) ; f(100).
b. Calculer les nombres x dont les images sont 2 400 ; – 45.
Exercice 20 :
Soit g la fonction linéaire telle que .
a. Quel est le coefficient de la fonction g ?
b. Calculer les images de 10 ; – 5 et 1.
c. Compléter les égalités suivantes :
g (10)= … g (- 5 ) = … et g(……)= – 0,4.
Exercice 21 :
On sait que 18 a pour image 23 par la fonction f et que 12 a pour image 14 par f.
f est-elle une fonction linéaire ?Pourquoi ?
Exercice 22 :
Exprimer la fonction linéaire f sous la forme ( le nombre a est à déterminer), puis calculer f(0) ; f(1) et f( – 2).
1. Lorsque l’image de 10 est – 3.
2. Lorsque f (- 100)= – 46.
3. Lorsque le coefficient de f est 2,5.
Exercice 23 :
Dans un repère,
a. Tracer la droite d représentant la fonction
b. Tracer la droite d d’équation .
Quelle fonction la droite d représente-t-elle ?
c. Tracer la droite d’ représentant la fonction linéaire g de coefficient a = – 2.
Exercice 24 :
Expliquer ce que signifie les notations suivantes :
a. .
b. .
Exercice 25 :
Parmi les fonctions données, indiquer celles qui sont affines, celles qui sont linéaires, celles qui ne sont pas affines.
Exercice 26 :
La fonction f est définie par : .
a. Calculer f(2) ;f(- 3) ; f(0).
b. Calculer l’image de 4.
c. Calculer le nombre x tel que :
.
Exercice 27 :
On donne les images de deux nombres par une fonction affine f.
f(3)=5 et f(7)=13
a. Tracer sa représentation graphique dans un repère.
b. Déterminer l’expression algébrique de cette fonction (c’est-à-dire déterminer a et b).
Exercice 28 – Problèmes
1. Dans un magasin, 100 g de chocolats sont vendus 3 €, et l’emballage coûte 1,52 €.
Sonia a acheté 750 g de chocolats et Samy en a achetés 900 g.
Combien chacun a-t-il payé ?
2. Deux personnes sont abonnées à un même ciné-club .
Pour trois séances, la première a payé 16 € (places et abonnement) ; pour cinq séances, la deuxième a payé 22 € ( places et abonnement).
Calculer le prix d’une place et le montant de l’abonnement.
Exercice 29 – Généralités sur les fonctions
Exercice 30 – Etude d’une fonction
Exercice 31 – Sens de variation
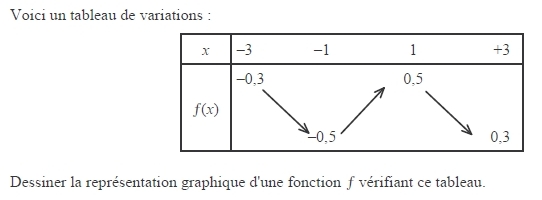
Exercice 32 – Tableau de variation
Exercice 33 – Etude d’une fonction rationnelle
On considère la fonction f définie par .
1. Déterminer son ensemble de définition.
2. Démontrer que f est une fonction positive sur .
3. Etudier la parité de la fonction f.
4. Tracer soigneusement la représentation graphique Cf de la fonction f.
5. Donner par lecture graphique la valeur du maximum de f sur :
a. l’intervalle [- 1;1].
b. l’intervalle [- 2;1].
6. Résoudre l’inéquation .
Exercice 34 – Image et antécédent
Soit définie sur
par
1. Calculer l’image de 0, l’image de 1 et l’image de par la fonction
.
2. Déterminer le (ou les) antécédent(s) de 3 par .
Exercice 35 – Image et antécédent par une fonction
est la fonction définie sur
par :
.
1. Calculer l’image de 2.
2. Calculer
3. Est-il vrai que 4 n’admet pas d’antécédent par ?
4. Est-il vrai que 0 admet un seul antécédent par ?
5. Déterminer un antécédent de – 12 .
Exercice 36 – Domaine de définition, image et antécédent
est la fonction définie sur
par :
1. Expliquer pourquoi n’est pas définie en
.
2. Calculer .
3. Déterminer l’antécédent de .
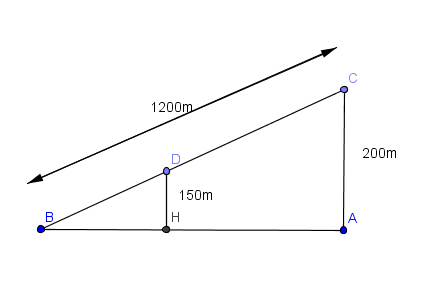
Exercice 37 – Skieur et théorème de Thalès
Un skieur dévale, tout schuss, une piste rectiligne représentée ci-dessous par le segment [BC] de longueur 1 200 m.
A son point de départ C, le dénivelé par rapport au bas de la piste, donné par la longueur AC, est de 200 m. Après une chute, il est arrêté au point D sur la piste.
Le dénivelé donné par la longueur DH, est alors de 150 M.
Calculer la longueur DB qu’il lui reste à parcourir.
Exercice 38 – Problème sur les fonctions
On fabrique une boîte à partir d’une feuille de carton carrée de 18 cm de côté .
On découpe à chaque coin du carré, un carré de côté x (cm) et on plie à 90° les bords libérés de façon à former une boîte de profondeur égale à x (cm).
On note x la largeur de l’encoche exprimée en cm, f(x) le volume de la boîte exprimée en cm cube.
1) Donner les valeurs possibles de x.
En déduire l’ensemble de définition D de f.
2) Donner l’expression de f sur D.
3) Représenter graphiquement cette fonction.
4) A l’aide du graphique, donner la valeur de x pour laquelle le volume de la boîte est maximal et établir le tableau de variations de la fonction f.
5) Montrer que f(x) – f(3) = 4 (x – 3)² (x – 12).
En déduire que f(x) est inférieur ou égal à f(3) pour tout x élément de [0;9]. Que peut-on en conclure ?









 Mathovore c'est 13 927 329 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 927 329 cours et exercices de maths téléchargés en PDF.