Des énoncés sur les généralités sur les fonctions afin de revoir ce chapitre du programme et s’exercer en ligne avec les fiches à imprimer au format PDF.
Exercice 1 – Lecture d’image et d’antécédent à partir d’un graphique
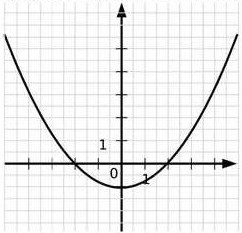
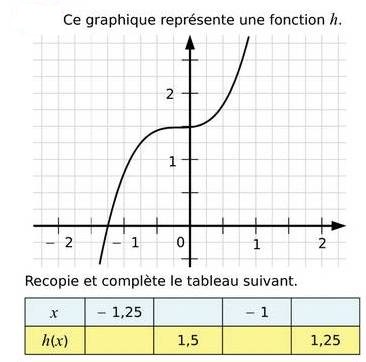
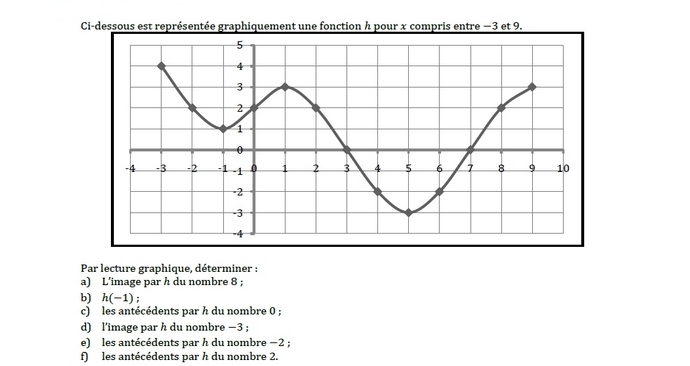
Ce graphique représente une fonction h.
a. Quelle est l’image de 0 par la fonction h ?
b. Quels nombres ont pour image 0 par la fonction h ?
c. Donner une valeur approchée de :
– l’image de 4 par la fonction h.
– l’image de – 3 par la fonction h.
Exercice 2 – Notion de fonctions, calcul d’image et d’antécédent
Exercice 3 – Problème sur les fractions
UNE BOITE EST FABRIQUEE DANS UNE PLAQUE DE CARTON CARREE DE 20 CM DE COTE. POUR CELA ON COUPE DES CARRES DE X CM ET ON PLIE LE LONG DES POINTILLES.
1. POURQUOI X EST COMPRIS ENTRE O ET 1O .
2. QUELLE EST LA HAUTEUR DE LA BOITE .
3. CALCULER L’AIRE A(x) DU CARRE AU FOND DE LA BOITE EN CM² .
4. CALCULER LE VOLUME V(x) DE LA BOITE EN CM3 .
5. REPRESENTER V(x) SUR UN GRAPHIQUE POUR LES VALEURS PRECEDENTES .
6. CONJECTURER LA VALEUR X POUR LAQUELLE LE VOLUME EST MAXIMUM .
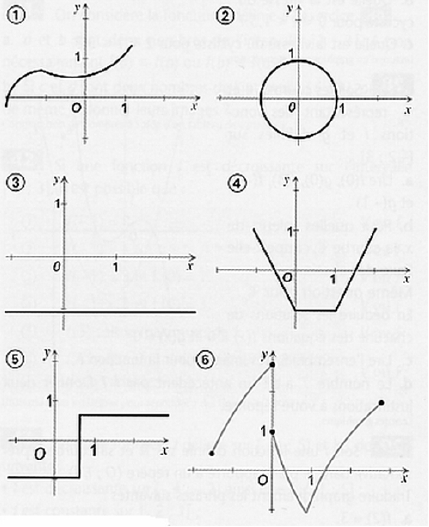
Exercice 4 – Courbes de fonctions ou pas
Dire si les représentations graphiques données sont, oui ou non, des représentations de fonctions :
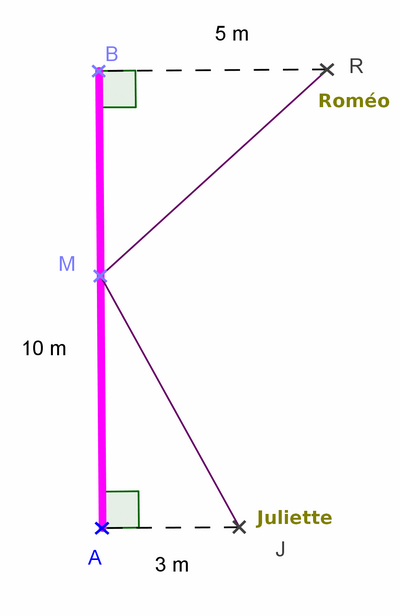
Exercice 5 – Roméo et Juliette
Roméo se trouve en R, Juliette en J.
Roméo doit aller cueillir une fleur sur le mur de roses [AB] et la porter à Juliette, le plus rapidement possible, donc par le chemin le plus court.
BR = 5 m , AJ = 3 m et AB=10 .
Déterminer la position du point M pour que son chemin emprunté soit le plus court.
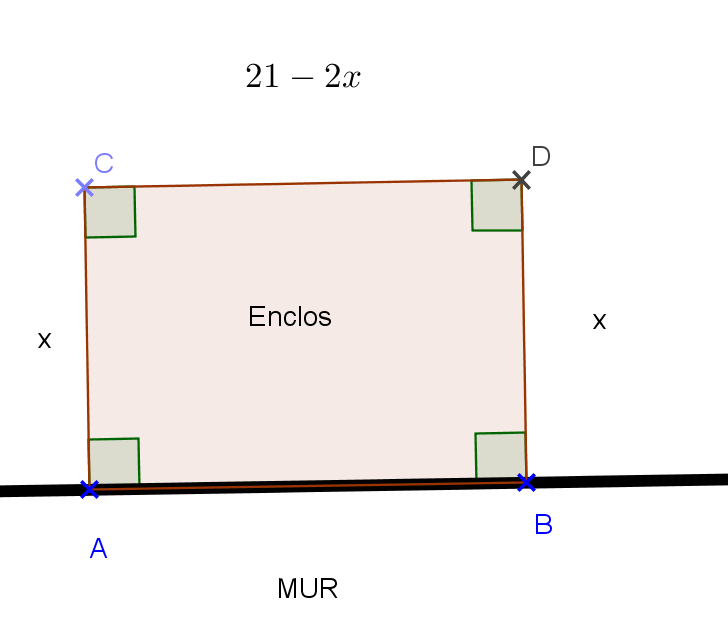
Exercice 6 – Enclos d’un chien
Pour son chien, Aicko, Mr Martin souhaite réaliser un enclos rectangulaire, le long de son mur.
Il dispose de 21 m de grillage.
Il veut utiliser les 21 m de grillage et donner le maximum d’espace pour Aicko.
1) a. Quelle est la longueur de l’enclos si son maître choisit une largeur de 3m ? de 7m ?
b. Quelle est l’aire dont dispose alors Aicko pour se débattre dans ces deux cas ?
2) Mr Martin souhaite que son chien ait le maximum d’espace.
Notons x la largueur de l’enclos.
a. Donner un encadrement de x (quelles sont les largeurs minimales et maximales ? )
b. Exprimer, en fonction de x, la longueur de l’enclos.
c. Prouver alors l’expression de l’aire de l’enclos en fonction de x, est .
Exercice 7 – Hauteur d’un triangle équilatéral
a. Calculer la hauteur puis l’aire d’un triangle équilatéral de côté 5 cm.
b. On note x le côté d’un triangle équilatéral (en cm).
Exprimer sa hauteur en fonction de x.
c. On appelle f la fonction qui à x associe l’aire d’un triangle équilatéral de côté x.
– Déterminer une expression de f.
– Calculer f ( 5 ) ; f ( 3 ) et .
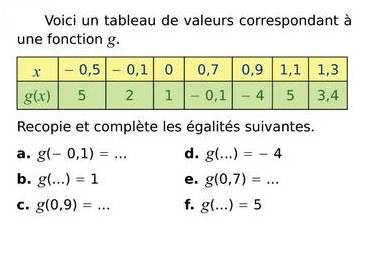
Exercice 8 – Compléter un tableau de valeur à l’aide d’une fonction
Exercice 9 – Tableau de valeurs et nombre d’antécédents
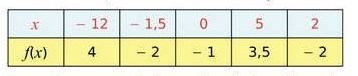
Le tableau suivant est un tableau de valeurs correspondant à une fonction f.
Dans chaque cas, indiquer, d’après le tableau, le (ou les) antécédents du nombre donné par la fonction f.
a. 3,5 b. – 2 c. 2
Exercice 10 – Courbe représentative d’une fonction
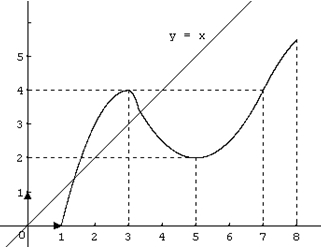
On a représenté ci-dessous :
· la droite d’équation y = x ,
· la courbe représentative d’une fonction f définie sur [1 ; 8].
Les questions posées seront résolues par lecture graphique.
1. Répondre par vrai ou faux aux questions suivantes :
| vrai ou faux | ||
| 1. | 1 a pour image 0 par la fonction f | |
| 2. | 0 a pour image 1 par la fonction f | |
| 3. | 7 est un antécédent de 4 par la fonction f | |
| 4. | 3 est un antécédent de 4 par la fonction f | |
| 5. | f (3) = 4 | |
| 6. | f (2) = 5 | |
| 7. | f (3) > f (5) | |
| 8. | 2,5 a trois antécédents par la fonction f | |
| 9. | 0,5 a un seul antécédent par la fonction f | |
| 10. | L’équation f ( x ) = 3 a au moins une solution
dans l’intervalle [1 ; 8] |
|
| 11. | L’équation f ( x ) = x a au moins une solution
dans l’intervalle [1 ; 8] |
|
| 12. | f est croissante sur l’intervalle [1 ; 8] | |
| 13. | Si x appartient à l’intervalle [4 ; 5], alors f ( x ) > x | |
| 14. | Si a et b appartiennent à l’intervalle [3 ; 5] et si a < b , alors f ( a ) < f ( b ) |
2. Résoudre graphiquement l’inéquation : f ( x ) – f (3) > 0. On donnera la solution sous forme d’un intervalle.
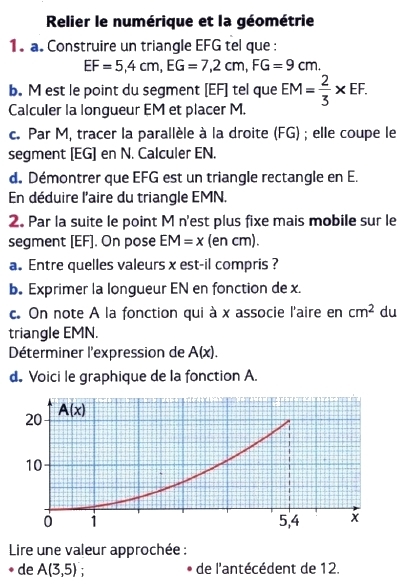
Exercice 11 – Géométrie
Exercice 12 – Thon pêché en Polynésie Française
Il existe trois variétés de thon pêché en Polynésie Française :
. le thon Germon (variété de thon blanc)
. le thon Jaune (à nageoires jaunes, variété de thon rouge)
. le thon Obèse (variété de thon rouge)
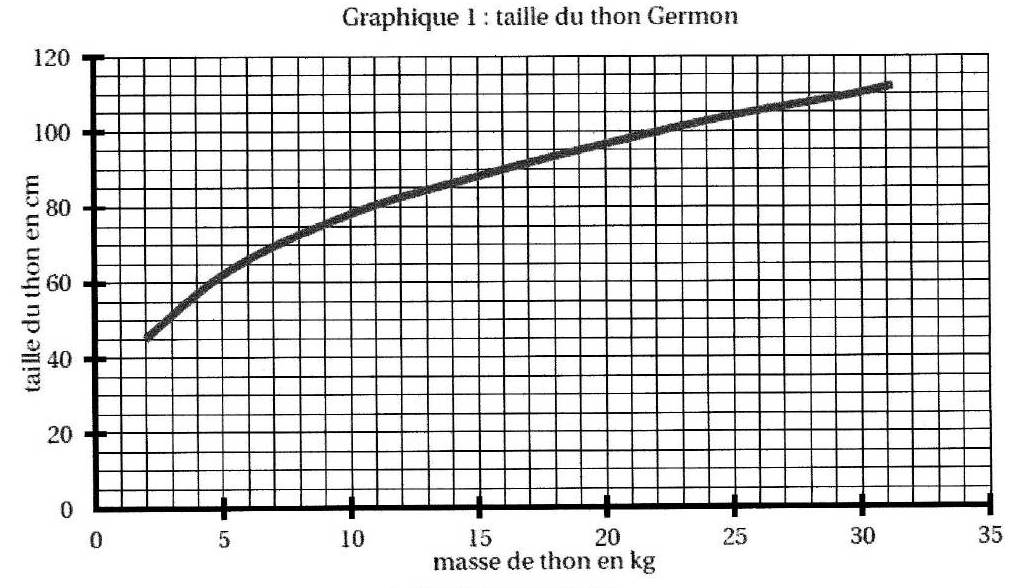
1. Le graphique 1, page suivante, représente la taille du thon Germon en fonction de sa masse.
a. Est-ce que la taille du thon germon est proportionnelle à sa masse ? Justifier.
b. L,équipe de Moana a capturé un thon Germon de 22 kg.Déterminer graphiquement, sa taille.
(On laissera apparents les trails de construction)-
c. L’équipe de Teiki a pris un thon germon de 70 cm. Déterminer graphiquement sa masse’
(On laissera apparents les traits de construction).
2. La masse du thon Jaune représente en moyenne 17% de la masse totale des trois espèces de thon
pêché.
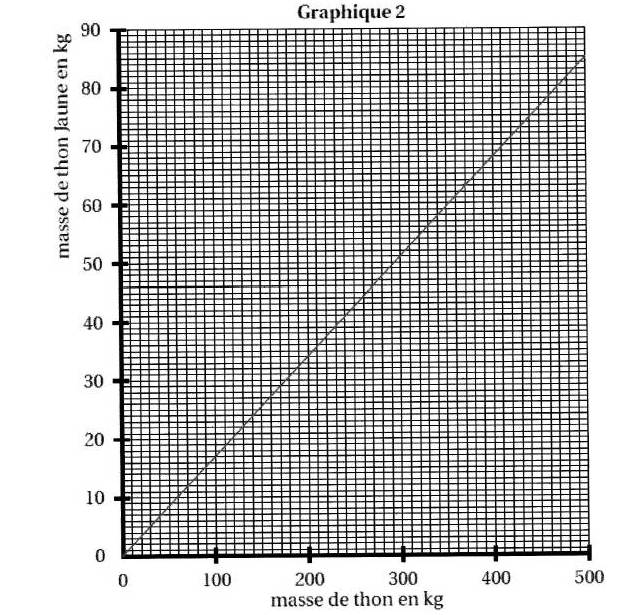
Le graphique 2 représente la masse de thon Jaune pêché par rapport à la masse totale de thon pêché.
a. Est-ce que la masse de thon Jaune est proportionnelle à la masse totale de thon pêché ? Justifier.
b. L,équipe de Moana a pêché 400 kg de thon.
Calculer la masse de thon Jaune pêché.
Exercice 13 – Représentation graphique d’une courbe
Exercice 14 – Exploitation d’une courbe





 Mathovore c'est 13 927 570 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 927 570 cours et exercices de maths téléchargés en PDF.