ˋLe périmètre et l’aire de figures géométriques à travers des exercices de maths en 5ème corrigés. Ces énoncés sont à télécharger en PDF. L’élève devra connaître ses formulés pour le carré, le rectangle, le losange, le parallélogramme et le trapèze en cinquième.
Exercice 1 – Calcul du périmètre d’une figure.
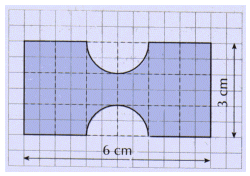
Calculer le périmètre de la figure ci-dessous.
Exercice 2 – Périmètre et aire d’une figure.
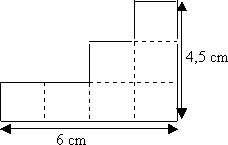
Calculer le périmètre et l’aire de la figure ci-dessous .
Exercice 3 – Calcul de l’aire d’une figure.
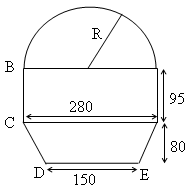
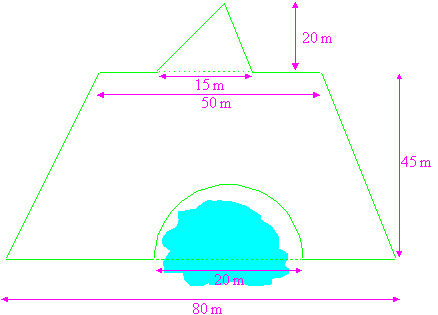
La figure est formée d’un trapèze, d’un rectangle et d’un demi-cercle (les longueurs sont en cm).
Calculer le rayon R du cercle.
Calculer l’aire du trapèze.
Calculer l’aire du rectangle.
Calculer l’aire du demi-disque.
Calculer l’aire totale.
Exercice 4 – Calcul de l’aire d’une figure géométrique.
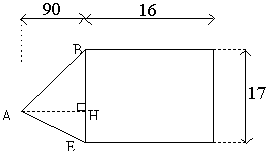
La figure est formée d’un rectangle et d’un triangle (les longueurs sont en mm).
Calculer l’aire du triangle, puis l’aire du rectangle, puis l’aire totale.
Exercice 5 – Pièce métallique.
Une pièce métallique à la forme d’un losange percé d’un trou de rayon 10.
Calculer l’aire hachurée.
Toutes les longueurs sont exprimées en cm.
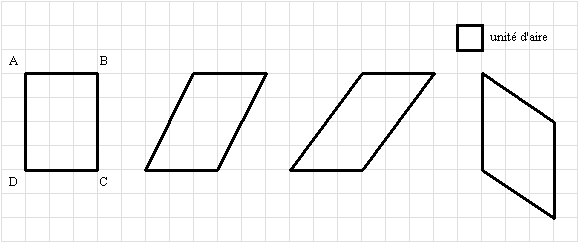
Exercice 6 – Aire de parallélogramme.
En prenant comme unité d’aire le carreau, donner l’aire du rectangle ABCD puis l’aire de chacun des parallélogrammes.
Exercice 7 – Unités d’aire et conversions
|
km² |
hm² |
dam² |
m² |
dm² |
cm² |
mm² |
|||||||
|
ha |
a |
ca |
|||||||||||
|
1 |
|||||||||||||
1 m² = 100 dm² = 10 000 cm² = 1 000 000 mm²
1 m² = 0,01 dam² = 0,000 1 hm² = 0,000 001 km²
ca = 1 m² 1 a = 1 dam² 1 ha = 1 hm²
1. Compléter :
360 cm² = 3,6 ………. 1 km² = 1 000 000 ……….. 10 000 m² = 1 ………….
8 m² = …… dm ² = ……cm² .
145 cm² = … m² = … mm²
0,1 dam ² = ……m² = …km²
2. Compléter :
15,4 m ² = ….dm ²
154 km² = … dm ²
0,02 cm² = …mm ²
2 024 mm² =…m ²
3,5 dam² = …… cm²
6 325 cm² = … m²
4,9 km² = … m²
3 060 mm² = …cm²
2,74 dm² = … cm²
58 830 cm² = … m²
0,68 cm² = … . mm²
46 000 m ² = … km ²
1 600 m ² =… km ²
172 mm ² = … cm ²
3 m ² = … cm ²
7,2 mm ² = … cm ²
3 ha = … m ²
18 ha = … cm²
856 ca = ……. m²
470 dm² = … a
8 400 a = … ha
3,5 km ² = …ha
18 a = … ha
0,0071 km ² = … a
1 m ² 35 dm ² = …dm ²
14 m ² 7 dm ² = …dm²
6 dam ² 8 m ² 29 dm ² = …dm²
480 cm² = …dm² ……cm²
14 506 cm² = …m² …dm² .…cm²
756 000 cm² =…..m² …dm²…cm²
7 dam ² = ……m² = 70 000 …..
6,2 m² = …dm² = 0,00062 …
Exercice 8 – Calcul de l’aire d’un rectangle.
Calculer l’aire des rectangles suivants :
Exercice 9 – Problème de surfaces et conversions d’aires.
L’inscription « 90 g/m² » sur une ramette de papier signifie
que 1 m² de ce papier pèse 90 g.
Combien pèse, en kg, une ramette de 500 feuilles de format A4
(rectangle de 21 cm x 29,7 cm) de ce papier ?
Exercice 10 – Calcul d’hauteur
Un triangle d’aire 0,1 dam² a un côté de longueur 800 cm.
Calculer la hauteur relative à ce côté .
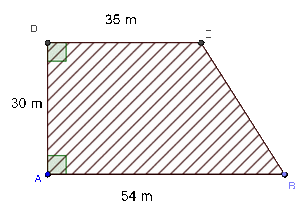
Exercice 11 – Aire d’un trapèze
Un champ a la forme d’un trapèze rectangle.
Calculer l’aire du champ.
Exercice 12 – Conversion de surfaces et tableau de conversion.
Compléter les aires et conversions suivantes :
a) 2,6 m²=……… dm²=…….cm²
b) 3 cm² = … dm² = … m²
c) ….. km² = 57,4 hm²= ….. m²
Exercice 13 – Calculer l’aire d’un pentagone.
Les longueurs sont données en centimètre.
Calculer l’aire du pentagone ABCDE suivant :
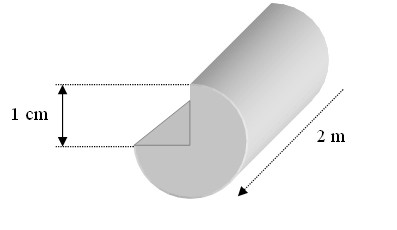
Exercice 14 – Surface peinte.
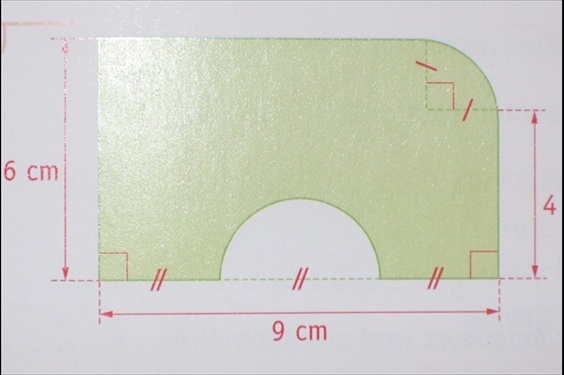
La forme de la base d’une moulure en bois brut de 2 m de long est dessinée ci-dessous.
On peint cette moulure, sauf les bases, de trois couches de peinture.
Calculer l’aire de la surface peinte.
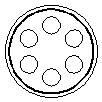
Exercice 15 – Bonde d’évacuation.
Une bonde d’évacuation d’un évier est formée d’un disque de 1,6 cm de rayon, percé de six trous identiques de 8 mm de diamètre.
Quelle est l’aire de cette bonde, au mm2 près ?
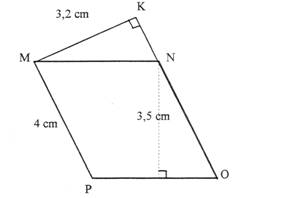
Exercice 16 – Calculer l’aire d’une figure géométrique.
1° Calculer l’aire du parallélogramme MNOP représenté ci-contre.
2° Calculer PO ( arrondir à 0,1 près ).
Exercice 17 – Calculer l’aire d’un parallélogramme.
La figure ci-dessous est un parallélogramme
1°Calcule son aire.
2° Calcule son périmètre.
Exercice 18 – Diamètre de la fusée Ariane
La fusée Ariane 5 mesure 57 m de haut.
a) Quelle est la hauteur de sa maquette à l’échelle ?
b) Le diamètre de la maquette est de 5,7 cm. Quel est le diamètre réel de la fusée ?.
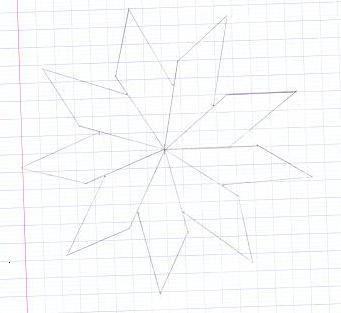
Exercice 19 – Périmètre d’un flocon
Calculer le périmètre de la figure suivante :
Exercice 20 – Calcul de hauteur.
Calculer la hauteur d’un triangle sachant que son aire est de 210 cm²
et la longueur de la base correspondante est de 21 cm.
Pour prendre un bon départ sur les formules d’aires
A – « L’intrus » :
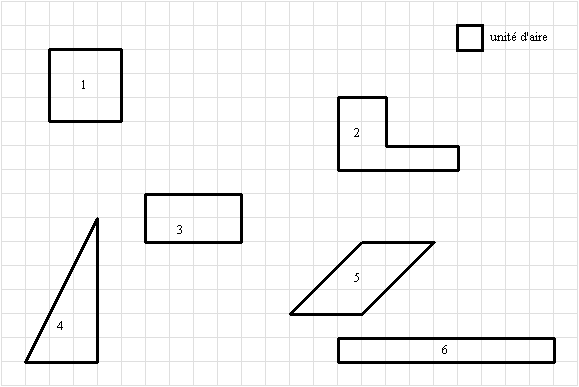
Sur le quadrillage ci-dessous, on a dessiné six figures.
Sachant que l’unité d’aire est le carreau, calculer l’aire de chacune des 6 figures et trouver ainsi l’intrus .
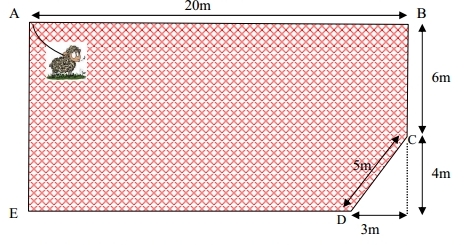
Exercice 21 – Aire et périmètre d’une parcelle.
Mr Léon possède un mouton.
Il l’a installé sur une parcelle verdoyante afin qu’il puisse brouter tranquillement.
Le plan de ce terrain est représenté ci dessous (partie colorée) :
1. Déterminer l’aire réelle de sa parcelle (on donnera les calculs) .
2. Mr Léon veut clôturer son terrain .
Quelle longueur réelle de grillage doit-il acheter sachant qu’il doit prévoir une ouverture de 1, 50 m pour un portail. ? (on donnera les calculs)
Le mouton est attaché au piquet A à l’aide d’une chaîne de 5m de long.
3. Représenter sur le plan la partie du terrain que peut brouter le mouton, hachurer-la en
vert.
Déterminer l’aire de la surface réelle broutée par le mouton).
On admettra que la partie du terrain broutée par le mouton a une aire de 4m².
Mr Léon doit traiter son terrain contre certains nuisibles.
4. Il ne veut pas traiter la partie sur laquelle le mouton se nourrit, déterminer alors l’aire de
la surface qu’il lui reste à traiter.
5. Sachant qu’il doit acheter 1 sachet de produit pour 30m², combien de sachets doit-il
acheter ?
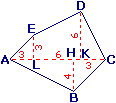
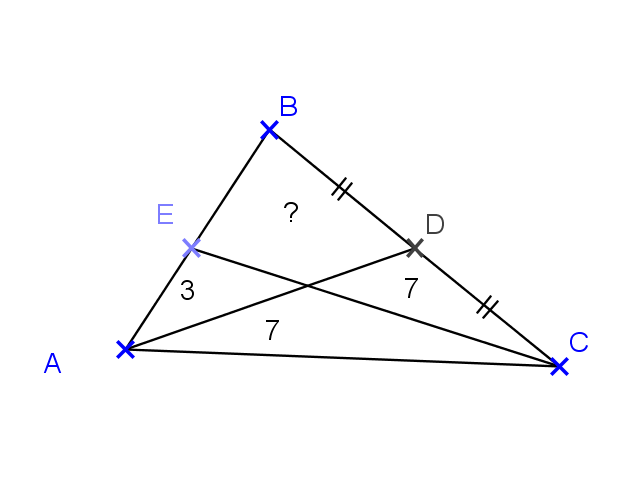
Exercice 22 – Aire d’une portion et médiane.
Le triangle ABC ci-dessous est partagé en 4 parties.
On connait les surfaces de trois d’entre elles:
- 3 unités d’aire;
- 7 unités d’aire;
- et 3 unités d’aire.
Quelle est la surface de la quatrième partie? justifier votre réponse.
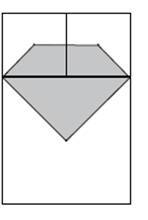
Exercice 23 – Problème ouvert sur le calcul d’aire, socle de compétences.
A partir de trois carrés et de leurs centres, on construit un pentagone.
Sachant que le côté du grand carré est de 4 cm,
quelle est l’aire du pentagone (zone grisée) ?
Exercice 24 – Aire d’une figure.
Calculer le périmètre et l’aire de cette figure.
Le résultat sera arrondi au
Exercice 25 – Calcul de l’aire d’un champ.
Calculer l’aire du champ suivant en
Exercice 26 – Calcul d’aire et de périmètre d’une figure.
Calculer l’aire et le périmètre de cette figure.
Les résultats seront arrondis au .
Exercice 27 – Dimensions d’un terrain de football.
Un terrain de football représenté à l’échelle est un rectangle de 23,1 cm de longueur sur 13,6 cm de largeur.
Quelles sont les dimensions réelles de ce terrain de football ?
Exercice 28 – Calculs d’aires de triangles et conversions d’aires
Effectuer les conversions :
a. 12m² en dm² b. 1,32dm² en cm² c. 4,5 cm² en m² d. 8 552m² en km²




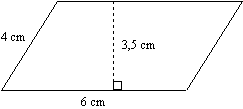





 Mathovore c'est 13 931 260 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 931 260 cours et exercices de maths téléchargés en PDF.