Exercice 1 – opération à trous
Pour chaque opération suivante, en montrant le calcul à effectuer, trouver le nombre manquant (on pourra poser les opérations à effectuer) :
|
45 + … = 128 |
312 – … = 267 |
… – 167 = 456 |
Exercice 2 – étude d’un parcours
Lisa doit encore parcourir 350 m pour arriver chez Samira, dont la maison se trouve à 800 m de la sienne.
Quelle distance Lisa a-t-elle déjà parcourue ?
Exercice 3 – problèmes à résoudre
1) En ajoutant 27 années à son âge, Estelle obtient l’âge de son père, c’est-à-dire 39 ans. Quel est l’âge d’Estelle ?
2) Sophie, la mère d’Estelle, a 2 ans de moins que son mari.
Quelle est la différence d’âge entre Estelle et sa mère ?
Exercice 4 – problème du monte-charge
Dans un restaurant, un monte-charge ne peut pas soulever plus de 50 kg. On pose sur ce monte-charge une caisse pesant 36,58 kg et une autre pesant 13,86 kg. Va-t-il pouvoir démarrer ?
Exercice 5 – problème de la planche
Une planche mesure 1,83 m. J’en coupe un morceau mesure 0,69 cm.
Quelle est la longueur restante ?
Exercice 6 – Problème de division
Exercice 7 – Problème et opérations
Vivien est un entraîneur dans un club de sport.
Il se rend dans un magasin pour faire des achats pour son club.
Certains éléments de sa facture ont été effacés. Aide-le à compléter sa facture .
| Quantité | Prix unitaire | Total | |
| Casquette | 5 | ………. | 60 € |
| Chaussure | 7 | ………. | 301 € |
| Polo | 9 | ………. | 252 € |
| Survêtement | 1 | ………. | ………. |
| Chaussette | ………. | 3 € | 195 € |
| TOTAL | 808 € |
Exercice 8 – Addition, soustraction, multiplication
Compléter les opérations suivantes :
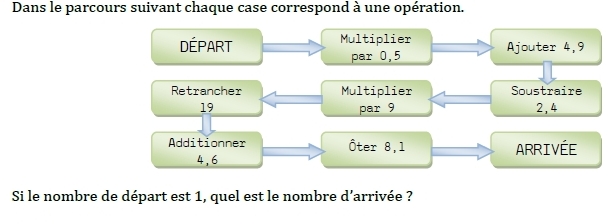
Exercice 9 – Parcours et opérations





 Mathovore c'est 13 931 213 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 931 213 cours et exercices de maths téléchargés en PDF.