Exercice 1 – écrire les rapports
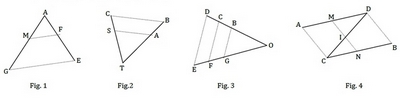
Dans chaque cas, écrire toutes les égalités des rapports de longueur du théorème de Thalès.
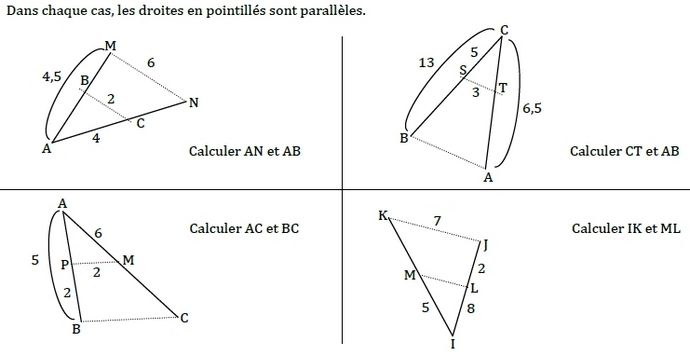
Les droites en pointillés sont parallèles.
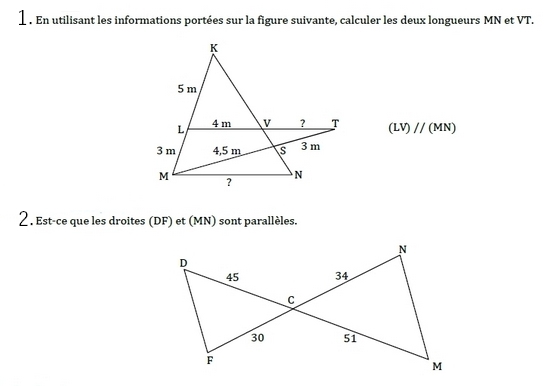
Exercice 2 – partie directe du théorème de Thalès
Exercice 3 – Contrefort et théorème de Thalès
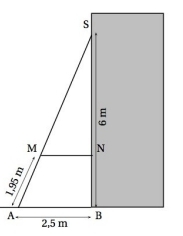
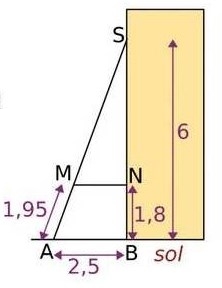
Pour consolider un bâtiment, on a construit un contrefort en bois.
Sur le dessin ci-dessous, on donne :
BS = 6 m ; BN = 1,8 m ; AM = 1,95 m ; AB = 2,5m.
1 En considérant que le montant [BS] est perpendiculaire au sol,
calculer la longueur AS.
2 Calculer les longueurs SN et SM.
3 Démontrer que la traverse [MN] est bien parallèle au sol.
Exercice 4 – Mur et théorème de Thalès
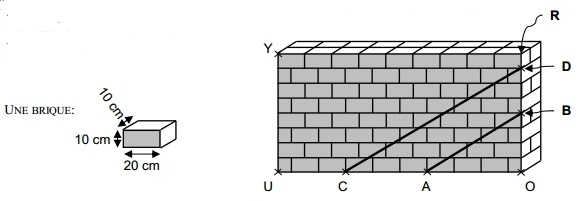
Le mur ci-dessous est constitué de briques de 10 cm sur 20 cm (et 10 cm de profondeur).
Il constitue le point d’appui d’une structure métallique.
Pour cela il est nécessaire d’avoir (AB) parallèle à (CD).
A-t-on (AB) parallèle à (CD) ?
Le démontrer.
Remarque:
Pour sceller (« coller ») les briques, il est nécessaire d’avoir du mortier.
On ne tiendra pas compte de cette épaisseur car elle est déjà incluse dans les 10 × 10 × 20 cm.
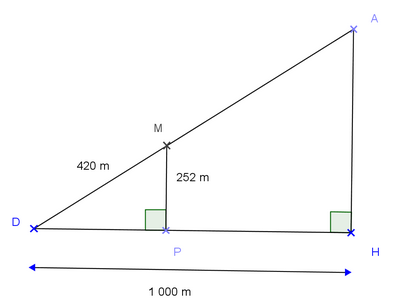
Exercice 5 – Funiculaire , théorème de Thalès et Pythagore.
Un funiculaire part de D pour se rendre à A suivant la droite (DA) .
DM = 420m ; DH = 1000m; MP = 252m.
Les triangles DPM et DAH sont respectivement rectangles en P et H.
1) Calculer la distance DP en mètre .
2) a) Démontrer que les droite (MP) et (HA) sont parallèles .
b) Calculer la distance DA en mètre puis en kilomètre.
Exercice 6 – Fabrication de boîtes par un artisan.
Un artisan fabrique des boîtes en forme de tronc de pyramide pour un confiseur.
Pour cela, il considère une pyramide régulière SABCD à base carrée où O est le centre du carré ABCD.
On a OA = 12 cm et SA = 20 cm.
a. Préciser la nature du triangle AOS et montrer que SO = 16 cm.
b. L’artisan coupe cette pyramide SABCD par un plan parallèle à la base tel que SM = 2cm où M est le centre de la section IJKL
ainsi obtenue.
Calculer le coefficient de réduction transformant la pyramide SABCD en la pyramide SIJKL.
c. En déduire la longueur SI puis la longueur IA.
Exercice 7 – Spectacle de marionnettes
Julien souhaite préparer un spectacle de marionnettes en ombres chinoises.
son écran mesure 2 m et sa marionnette mesure 24 cm.
Perché sur une estrade, il tient sa marionnette à 30 cm de la lumière, placée sous l’estrade.
A quelle distance de la source de lumière doit-il placer l’écran pour agrandir sa marionnette au maximum ?
Une deuxième série d’exercices sur le théorème de Thalès en 3ème.
Exercice 8 – Consolidation d’un bâtiment
Pour consolider un bâtiment, des charpentiers ont construit un contrefort en bois.
Sur le schéma ci-dessous, les mesures sont en mètre.
a. En considérant que le montant [BS] est perpendiculaire au sol, calculer la longueur AS.
b. Calculer les longueurs SM et SN.
c. Démontrer que la traverse [MN] est bien parallèle au sol.
Exercice 9 – Parcours dans les bois
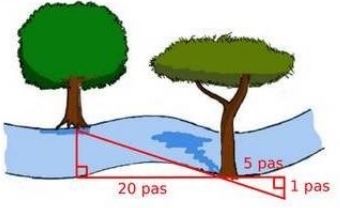
Par un beau dimanche ensoleillé, Julien se promène au pied de la montagne Sainte Victoire au bord de la rivière Arc.
Il se demande quelle est la largeur de cette rivière.
Il prend des repères, compte ses pas et dessine le schéma ci-dessous.
a. Quel est, en nombre de pas, la largeur de la rivière qu’obtient approximativement Julien ?
b. Julien estime la longueur de son pas à 65 cm.
Donner une valeur approximative de la largeur de cette rivière au centimètre près.
Exercice 10 – Sports d’hiver.
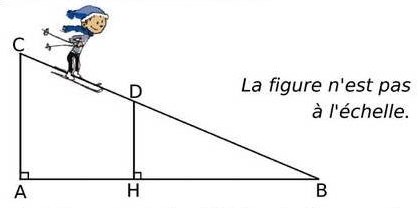
Un skieur dévale, tout schuss, une piste rectiligne représentée ci-dessous par le segment [BC] de longueur 1 200 m.
A son point de départ C, le dénivelé par rapport au bas de la piste, donné par la longueur AC, est de 200 m.
Après une chute, il est arrêté au point D sur la piste.
Le dénivelé, donné par la longueur DH, est alors de 150 m.
Calculer la longueur DB qu’il lui reste à parcourir.
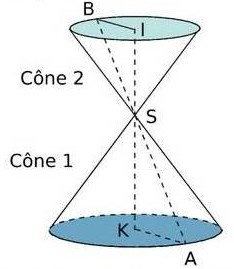
Exercice 11 – Deux cônes de révolution
Les deux cônes de révolution de rayons KA et IB sont opposés par le sommet.
Les droites (AB) et (KI) se coupent en S, et de plus (BI) et (KA) sont parallèles.
On a KA = 4,5 cm ; KS = 6 cm et SI = 4 cm.
Calculer la longueur BI.
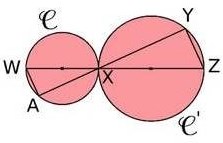
Exercice 12 – Utilisation du théorème de Thalès
Peut-on utiliser le théorème de Thalès dans les figures ci-dessous ?
justifier votre réponse.
e. [WX] est un diamètre du cercle et [XZ] est un diamètre du cercle
.
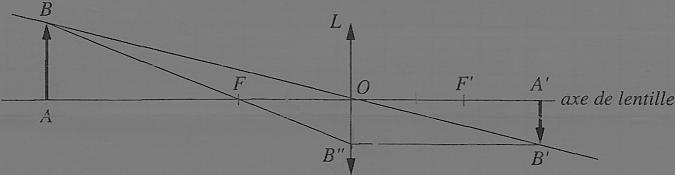
Exercice 13 – Lentilles convergentes et Thalès
Le schéma ci-dessus représente un objet [AB] et son image [A’B’] donnée par
une lentille convergente L.
Les points F et F’ sont les foyers de la lentille : OF = OF’ = 3 cm.
La droite (B’B ») est parallèle à l’axe de la lentille.
L’objet [AB] mesure 2,5 cm et est placé perpendiculairement à l’axe.
Le point A est placé à 8 cm de celle-ci et les points B, O et B’ sont alignés.
Calculer la hauteur A’B’ de l’image et sa position OA’.
Exercice 14 – Distance terre lune.
Mr Fantastic a un bras long de 2,80m.
Il peut ainsi masquer parfaitement la lune, avec une pièce de 3 euros, de 26 mm de diamètre, lorsqu’il la tient au bout de son bras tendu.
Sachant que le rayon de la lune est de 1737km,
Calculer la distance Terre-Lune arrondie au km.
Exercice 15 – Configuration du sablier.
On considère les points A,I et C alignés dans cet ordre et les points D,I et F alignés dans cet ordre.
On donne IF = 7;IC = 5x; IA = 7x + 5; ID = 12.
Déterminer la valeur de x pour laquelle les droites (FC) et (DA) sont parallèles.
Exercice 16 – Hauteur d’un bâton
un bâton est placé verticalement contre un mur. si on écarte le pied de ce bâton de 45 cm du bas du mur, son sommet glisse de 15cm vers le bas.
Quelle est la longueur de ce bâton ?
Exercice 17 – Problème sur le théorème de Thalès.
Construire un triangle ABC tel que AB=12cm,BC=16cm,AC=8cm .
1)Placer le point E sur (AB) tel que AE=9cm puis tracer la parallele à (BC) passant par E.Elle coupe (AC) en F. Calculez AF.
2)Dans la suite du problème,le point E se promene sur (AB) et on pose AE=x .
a)Donner un encadrement de x .
b)Calculer AF en fonction de x .
c) En déduire FC et exprimer également EB en fonction de x .
3)La parallele à (AB) passant par F coupe (BC) en K .
a)Calculer BK en fonction de x .
b)Quelle est la naute du quadrilatere EFBK ? en déduire EF .
Exercice 18 – Théorème de thalès et sa réciproque.
ABC est un triangle tel que : AB= 8cm ; AC= 6,4cm et BC= 4,9 cm .
Le point E appartient à la demi-droite [AB) et : AE= 12cm .
Le point F appartient à la demi-droite [AC) et : AF= 9,6cm .
a) Calculer L’angle  .
b) Quelle est la nature du triangle AEF ? Justifier votre réponse.
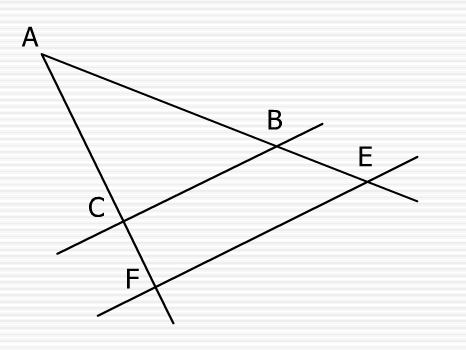
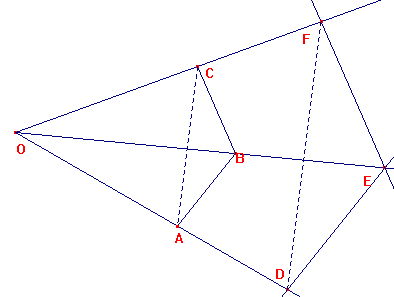
Exercice 19 – Une configuration de Desargues
Les points O,C,F ; O,B,E et O,A,D sont alignés.
(CB)//(FE) et (BA)//(ED).
Montrer que (CA)//(FD) .
Exercice 20 – Réciproque du théorème de Thalès.
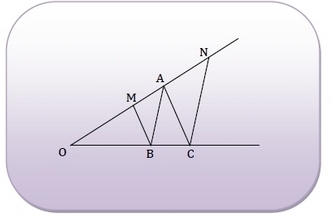
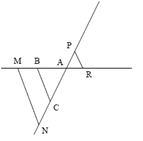
Exercice 21 – Théorème de Thalès.
On sait que (BM) // (AC) et que (AB) // (NC).
Montrer que .
Exercice 22 – Théorème de Thalès et problèmes
L’unité est le centimètre.
Dans la figure ci-dessous, les droites (AB) et (CD) sont parallèles.
Les droites (AD) et (BC) se coupent en E.
On donne DE = 6, AE = 10, AB = 20 et BE = 16.
Les deux figures de cette page ne sont pas réalisées en vraie grandeur.
Elles ne sont pas à reproduire.
1. Calculer la distance CD.
Les points F et G appartiennent respectivement aux segments [BC] et [AB].
Ils vérifient : BF = 12,8 et BG = 16.
2.Montrer que les droites (FG) et (AE) sont parallèles .
Exercice 23 – Applications du théorème de Thalès.
On précisera pour chacune des deux questions de cet exercice la propriété de cours utilisée.
La figure ci-dessous n’est pas représentée en vraie grandeur.
Les droites (BC) et (MN) sont parallèles.
On donne :
AB 2,4 cm ; AC = 5,2 cm ;
AN = 7,8 cm et MN = 4,5 cm.
1. Calculer les longueurs AM et BC.
2. Sachant que AP = 2,6 cm et AR = 1,2 cm .
Montrer que les droites (PR) et (BC) sont parallèles.
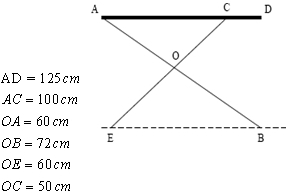
Exercice 24 – Problème de la planche.
Le segment [AD] représente la planche.
Les segments [AB] et [EC] représentent les pieds.
Les droites (AB) et (EC) se coupent en O.
On donne :
1. Montrer que la droite (AC) est parallèle à la droite (EB).
2. Calculer l’écartement EB en cm.
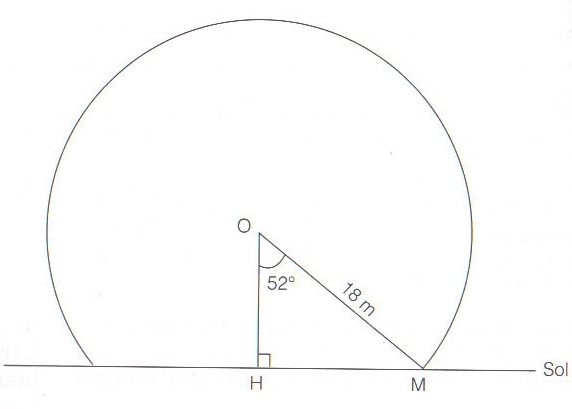
Exercice 25 – Problème de la géode.
Dans le parc de la cité des sciences se trouve la Géode, salle de cinéma qui a, extérieurement, la forme d’une calotte sphérique posée sur le sol, de rayon 18 m.
1. Calculer OH .
2. Calculer HM ( donner le résultat arrondi à 1 m près).
3. calculer la hauteur totale de la géode .
4. a. Quelle est la forme de la surface au sol occupée par la géode ?
b. Calculer l’aire de cette surface (arrondir le résultat à 1 m² près) .
5. On veut représenter le triangle OMH à l’échelle .
a. Quelle est la longueur Om sur cette représentation ?
Construire le triangle OMH à l’échelle .
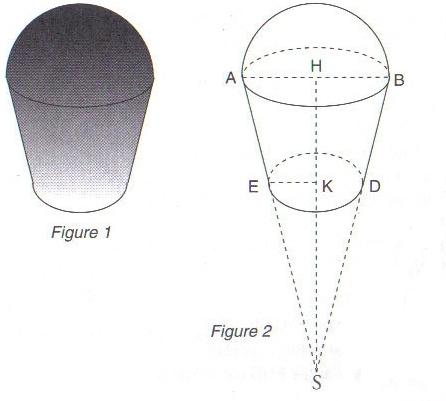
Exercice 26 – Le pommeau de vitesse.
La figure 1 représente le pommeau de levier de vitesse d’une automobile .
Il a la forme d’une demi-boule surmontant un cône dont on a sectionné l’extrémité comme l’indique la figure 2 .
On appelle le cône dont la base est le cercle de rayon [AH] et
le cône dont la base est le cercle de rayon [EK].
Ces deux cercles sont situés dans des plans parallèles .
• Rappel des formules :
Volume d’un cône :
Volume d’une boule :
On pose : Sk = 4 cm ; SH=10 cm ; AH = 2 cm .
1. En se plaçant dans le triangle SAH, calculer la tangente de l’angle .
En déduire une valeur approchée, à un degré près, de l’angle .
2. En se plaçant dans le triangle rectangle ESK et en utilisant la tangente de l’angle , montrer que : EK= 0,8 cm .
3.a. Calculer les volumes et
des cônes
et
.
On donnera des valeurs approchées pour les deux calculs de volumes demandés au près .
b. Calculer le volume de la demi-boule ; en donner une valeur approchée au
près .
c. Déduire des résultats précédents une valeur approchée du volume du pommeau .
Exercice 27 – Problème du puits.
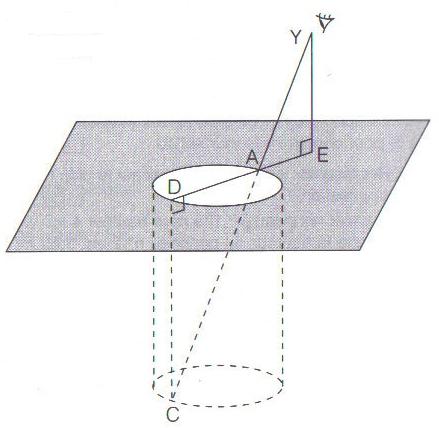
[AD] est un diamètre d’un puits de forme cylindrique .
Le point C est à la verticale de D, au fond du puits .
Une personne se place en un point E de la demi-droite [DA) de sorte que ses yeux soient alignés avec les points A et C.
On note Y le point correspondant aux yeux de cette personne.
On sait que :
AD = 1,5 m ; EY=1,7 m ; EA=0,6 m .
1.Démontrer que les droites (DC) et (EY) sont parallèles .
2. Calculer DC, la profondeur du puit.
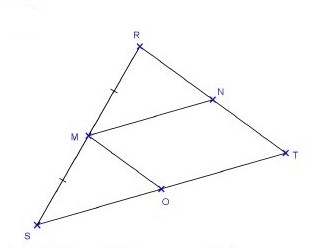
Exercice 28 – Droite des milieux et ses propriétés
Les droites (MO) et (RT) sont parallèles.
Montrer que O est le milieu de [ST].
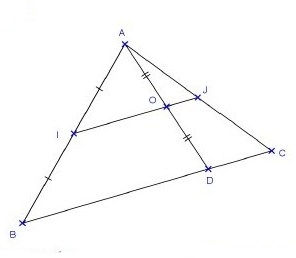
Exercice 29 – Propriétés et droite des milieux
1. Montrer que les droites (IO) et (BD) sont parallèles.
2. Montrer que J est le milieu de [AC].







 Mathovore c'est 13 927 216 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 927 216 cours et exercices de maths téléchargés en PDF.