Nombres complexes : exercices de maths en terminale corrigés en PDF.

Mis à jour le 29 mai 2025

Sommaire

✏️Exercices

Terminale • Lycée

Nombres complexes

⏱️ Temps de travail : 20-45 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Les nombres complexes à travers des exercices de maths en terminale corrigés faisant intervenir la notion de conjugué, d’argument, les formules de Moivre et d’Euler ainsi que les écritures arithmétiques et géométriques.

Exercice 1 :
Mettre les nombres complexes sous la forme a + ib (a et b réels).

$\frac{1}{i}$
$\frac{3+2i}{1-i}$
$1+\frac{i-1}{i+1}$
$\frac{1+2i}{(2+i)(2-\sqrt{3}i)}$

Exercice 2 :
Soit z=x+iy un nombre complexe (x et y réels).
On demande de calculer la partie réelle et la partie imaginaire de Z puis de déterminer l’ensemble des points M d’affixe z tels que Z soit réel ou imaginaire pur.

$Z=\frac{z-i}{z+1-2i}$
$Z=\frac{i(z+1)}{z-2i}$
$Z=\frac{2+\overline{z}}{1+\overline{z}}$

Exercice 3 :

Soit $j=-\frac{1}{2}+i\frac{\sqrt{3}}{2}$ .
Calculer

Exercice 4 : théorème de Von Aubel.

On considère un quadrilatère ABCD de sens direct.
On construit quatre carrés de centres respectifs P, Q, R et S qui s’appuient extérieurement sur les côtés [AB], [BC], [CD] et [DA] du quadrilatère ABCD (voir figure).
Le but du problème est de démontrer que les diagonales du quadrilatère PQRS sont perpendiculaires et de même longueur.

On note a, b, c, d, p, q, r et s les affixes respectives des points A, B, C, D, P, Q, R et S dans un repère orthonormé $(O,\vec{e_1},\vec{e_2})$ de sens direct.

Démontrer que dans le carré construit sur [AB], on a $p=\frac{a-ib}{1-i}$ .
Etablir des relations analogues pour p, q, r et s en raisonnant dans les trois autres carrés.
Calculer $\frac{s-q}{r-p}$ puis conclure.

Exercices 5 : théorème de Napoléon.
On munit le plan d’un repère $(O,\vec{e_1},\vec{e_2})$ de sens direct.

Partie A : des caractérisations du triangle équilatéral.
On note $j=e^{\frac{2i\pi}{3}}$ .Soient U, V et W trois points du plan d’affixes respectives u, v, w.

Démontrer l’équivalence suivante : UVW est équilatéral de sens direct $\Leftrightarrow,u-v=-j^2(w-v)$ .
Démontrer l’équivalence suivante : UVW est équilatéral de sens direct $\Leftrightarrow,u+jv+j^2w=0$ .

Partie B : démonstration du théorème de Napoléon.

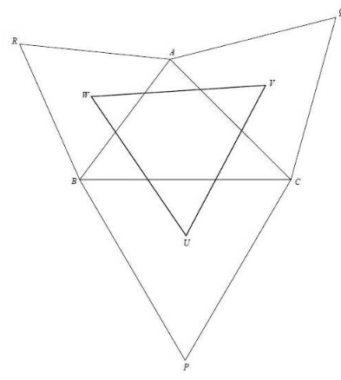
ABC est un triangle quelconque de sens direct.

On construit les points P, Q et R tels que BPC, CQA et ARB soient des triangles équilatéraux de sens direct.
On note U, V, W les centres de gravité de BPC, CQA et ARB respectivement.
Démontrer que UVW est équilatéral de même centre de gravité que ABC.

Exercice 6 : montrer qu’un complexe est un réel ou imaginaire pur.
Démontrer les équivalences suivantes :

$Z\,reel\Leftrightarrow,Z=\overline{Z}$ .
$Z\in\mathbb{R}\Leftrightarrow,(Z=0\,ou\,arg(Z)=0[\pi])$ .
$Z\,imaginaire\,pur\Leftrightarrow,Z+\overline{Z}=0$ .

Exercice 7 : racines de l’unité et applications.
Soit un entier naturel.

On appelle racine nièmes de l’unité tout nombre complexe tel que z^n=1 .
On note U_n l’ensemble des racines nièmes de l’unité.Par exemple $U_2=,\{,-1;1,,\}$ .
1.Démontrer que $U_n={e^{\frac{2ik\pi}{n}},k\in,\{,0,1,2,...,n-1,,\}}$ .
démontrer que la somme des racines nièmes de l’unité est nulle.
Démontrer que, dans un repère orthonormal direct $(O,\vec{e_1},\vec{e_2})$ , les images des nombres $w_k={e^{\frac{2ik\pi}{n}},}$ sont les sommets d’un polygone régulier.

Exercice 8 : lieu de points.
Soit z un nombre complexe différent de 1.On note M le point du plan complexe d’affixe z.
On pose $Z=\frac{z+1}{z-1}$ .
Déterminer l’ensemble :
1.E des points M tels que Z soit réel.
2.F des points M tels que $\,|Z\,\,|=1$ .
3.G des points M tels que $arg(Z)=\frac{\pi}{2}[2\pi]$ .

Exercice 9 : identité du parallélogramme.
Démontrer que pour tous nombres complexes Z et Z ‘, on a :
$,|Z+Z'\,\,|^2+\,|Z-Z'\,\,|^2=2,|Z\,,|^2+2\,|Z'\,\,|^2$

Indication : utiliser la relation $\,|Z\,|^2=Z\overline{Z}$
Interpréter géométriquement.

Exercice 10 : utilisation des nombres complexes.
Soient a, b nombres entiers relatifs.On suppose que a et b sont la somme de deux carrés :
il existe x, y $\in,\mathbb{Z}$ tels que et il existe $z,t\in,\mathbb{Z}$ tels que .
Démontrer que le produit ab est encore la somme de deux carrés.

Indice : écrire .

Exercice 11 : écriture complexe d’une transformation.
1. Soit f la transformation du plan complexe qui à M(z) associe M ‘ (z) tel que .
Déterminer la nature et les éléments caractéristiques de f lorsque a = 2, puis lorsque a = – i.
2. On donne A(1), B(2+i), A ‘ (2i) et B ‘ (1+i).
Vérifier que AB=A’B’.
Démontrer qu’il existe une unique rotation r telle que r(A) = A’ et r(B) = B’.La déterminer..

Exercice 12 : calcul de cosinus et sinus.
1.Résoudre dans $\mathbb{C}\,\times \,\mathbb{C}$ , le système suivant :
$\{\begin{matrix},u+v,=-\frac{1}2{,\\,uv=-\frac{1}{4} \,\end{matrix}.$
2. On pose $w=e^{\frac{2i\pi}{5}}$ .
Démontrer que .
En déduire, à l’aide des formules d’Euler, que :
$cos\,(\,\frac{2\pi}{5}\,\,)+cos\,(\,\frac{4\pi}{5}\,\,)=-\frac{1}{2}$

Exercice 13 : extrait du bac.
Soient les nombres complexes $z_1=\frac{\sqrt{6}-i\sqrt{2}}{2}$ et z_2=1-i .
1. Mettre sous forme trigonométrique $z_1\,,\,z_2\,,\,Z=\frac{z_1}{z_2}$ .
En déduire que :
$cos(\frac{\pi}{12})=\frac{\sqrt{6}+\sqrt{2}}{4}$ et $sin(\frac{\pi}{12})=\frac{\sqrt{6}-\sqrt{2}}{4}$ .
3. On considère l’équation d’inconnue réelle x :

$(\sqrt{6}+\sqrt{2})cos x+(\sqrt{6}-\sqrt{2})sin x=2$ .

a. Résoudre cette équation dans $\mathbb{R}$ .
b. Placer les points images des solutions sur le cercle trigonométrique .

Exercice 14 – Somme de modules
On considère un nombre complexe z de module 1 (|z|=1)
Montrer que :
|1 + z|² + |1 – z|² = 4

Exercice 15 -Forme algébrique
I.1)Quelle est la forme la forme algébrique de $\sqrt{2}e^{i\frac{\pi }{2}}e^{i\frac{\pi }{4}}$ ?
2) Quelle est la forme algébrique de $\frac{2}{3}\frac{e^{i\frac{\pi }{2}}}{e^{i\frac{\pi }{3}}}$ ?
II.1)Factoriser astucieusement Z = z²+9
2)Idem Z=z²+5
3)Z = z²+1.

III.1) Quelle est la transformation associée à la fonction $z \mapsto z+a$ avec z et a appartenant à $\mathbb{C}$ , z de la forme x+iy, x, y appartiennent à $\mathbb{R}$
2) Quelle est la transformation associée à la fonction $z \mapsto -z$ avec z appartient à $\mathbb{C}$
3) Quelle est la transformation associée à la fonction $z \mapsto iz$ avec z appartient à $\mathbb{C}$

Exercice 16 -Nombres complexes extrait de sujet du bac S
Le plan complexe est rapporté est rapporté à un repère orthonormal $(O,\vec{u},\vec{v})$

Soit (C ) le cercle de centre O et de rayon 1.
On considère le point A de (C ) d’afﬁxe $z_A=e^{i\frac{\pi}{3}}$

1) Déterminer l’afﬁxe z_B du point B image de A par la rotation de centre O et d’angle $\frac{2\pi}{3}$ .

Déterminer l’afﬁxe z_C du point C image de B par la rotation de centre O et d’angle $\frac{2\pi}{3}$ .

2. a) Justiﬁer que (C ) est le cercle circonscrit au triangle ABC.
Construire les points A, B et C sur la feuille de papier millimétré.

b) Quelle est la nature du triangle ABC ? Justiﬁer.

3) Soit h l’homothétie de centre O et de rapport −2.

a) Compléter la ﬁgure en plaçant les points P, Q et R images respectives des points A, B et C
par h.

b) Quelle est la nature du triangle P QR ? Justiﬁer.

4) Dans cette question, le candidat est invité à porter sur sa copie les étapes de sa démarche
même si elle n’aboutit pas.

a) Donner l’écriture complexe de h.

b) Calculer .

En déduire que A est le milieu du segment [QR].

c) Que peut-on dire de la droite (QR) par rapport au cercle (C ) ?

Exercice 17 :
Le plan complexe est rapporté au repère orthonormal direct $(O,\vec{u},\vec{v})$ .

On prendra pour le dessin $\| \vec{u} \|=4\,cm.$

M est un point d’afﬁxe z non nul.
On désigne par M′ le point d’afﬁxe $z'=-\frac{1}{z}$ .

où z désigne le conjugué du nombre complexe z.

Partie A. Quelques propriétés

1) Soit z un nombre complexe non nul.
Déterminer une relation entre les modules de z et z′, puis
une relation entre les arguments de z et z′.

2) Démontrer que les points O, M et M′ sont alignés.

3) Démontrer que pour tout nombre complexe z non nul, on a l’égalité :

$\overline{z'+1}=\frac{1}{z}(z-1)$

Partie B. Construction de l’image d’un point

On désigne par A et B les deux points d’afﬁxes respectives 1 et −1.

On note C l’ensemble des points M du plan dont l’afﬁxe vériﬁe :

|z − 1| = 1.

1) Quelle est la nature de l’ensemble C ?

2) Soit M un point de C d’afﬁxe z, distinct du point O.

a) Démontrer que |z′ + 1| = |z′|.

Interpréter géométriquement cette égalité.

b) Est-il vrai que si z′ vériﬁe l’égalité |z′ + 1| = |z′’|, alors z vériﬁe l’égalité |z − 1| = 1 ?

3) Tracer l’ensemble C sur une figure.
Si M est un point de C , décrire et réaliser la construction du point M′ .
.

Exercice 18 -Nombres complexes Bac S Pondichéry
Cet exercice contient une restitution organisée de connaissances.

Partie A

On suppose connus les résultats suivants :

1. Dans le plan complexe, on donne par leurs afﬁxes z_A , z_B et z_C trois points A, B et C.

Alors $|\frac{z_B-z_C}{z_A-z_C} |=\frac{CB}{CA}\,et\,arg ( \frac{z_B-z_C}{z_A-z_C} )=(\vec{CA},\vec{CB})\,\,[2\pi]$

2. Soit z un nombre complexe et $\alpha$ un réel : $z=e^{i\theta }$

si et seulement si |z| = 1 et arg(z) = θ + 2kπ, où
k est un entier relatif.

Démonstration de cours :

Démontrer que la rotation r d’angle α et de centre Ω d’afﬁxe ω est la

transformation du plan qui à tout point M d’afﬁxe z associe le point M′ d’afﬁxe z′

tel que $z'-w=e^{i\alpha }(z-w)$

Partie B

Dans un repère orthonormal direct du plan complexe $(O,\vec{u},\vec{v})$ d’unité graphique 2 cm,
on considère les points A, B, C et D d’afﬁxes respectives :

$z_A=-\sqrt{3}-i\,;\,z_B=1-i\sqrt{3},z_C= \sqrt{3}-i,z_D=-1+i \sqrt{3}$

3.
1. a. Donner le module et un argument pour chacun des quatre nombres complexes z_A , z_B , z_C et z_D .

b. Comment construire à la règle et au compas les points A, B, C et D dans le repère $(O,\vec{u},\vec{v})$ ?
c. Quelle est la nature du quadrilatère ABCD ?

2. On considère la rotation r de centre B et d’angle $-\frac{\pi}{3}$ .
Soient E et F les points du plan déﬁnis par : E = r(A) et F = r(C).

a. Comment construire à la règle et au compas les points E et F dans le repère précédent ?

b. Donner l’écriture complexe de r.

c. Déterminer l’afﬁxe du point E.

Exercice 19 -Equations complexes Bac S France

Le plan complexe est rapporté au repère orthonormal $(O,\vec{u},\vec{v})$ ; l’unité graphique est 1 cm.

1) Résoudre, dans l’ensemble des nombres complexes, l’équation :

On donnera les solutions sous forme algébrique, puis sous forme trigonométrique.

2) On note A et B les points du plan d’afﬁxes respectives :

a = 2 − 2i et b = −a.

a) Déterminer l’afﬁxe c du point C, image du point B par la rotation de centre O et d’angle $\frac{\pi}{2}$ .

b) On note D l’image de C par la rotation de centre A et d’angle $\frac{\pi}{2}$ .

Démontrer que l’afﬁxe d du point D est d = 2 − 6i.

c) Placer les points C et D sur le graphique.
Quelle est la nature du quadrilatère ABCD ?

3) $\alpha$ étant un nombre réel non nul, on désigne par $G_\alpha$ le barycentre du système :

{(A, 1),(B, −1),(C, $\alpha$ )}.

a) Exprimer le vecteur $\vec{CG_\alpha }$ en fonction du vecteur $\vec{BA}$ .

b) En déduire l’ensemble des points $G_\alpha$ lorsque $\alpha$ décrit l’ensemble des réels non nuls.

Construire cet ensemble.

c) Pour quelle valeur de $\alpha$ a-t-on $G_\alpha$ = D ?

4) On suppose dans cette question que $\alpha$ = 2.

Dans cette question, toute trace de recherche, même incomplète, ou d’initiative non fructueuse, sera
prise en compte dans l’évaluation.

Déterminer et construire l’ensemble des points M du plan tels que :

$\| \vec{MA}-\vec{MB}+2\vec{MC} \|=4\sqrt{2}$

Exercice 20 -Etude d’une application
La feuille annexe donnée portera les constructions demandées au cours de l’exercice.

Dans le plan complexe rapporté au repère orthonormal direct $(O,\vec{u},\vec{v})$ , le point A a pour afﬁxe i.
On nomme f l’application qui, à tout point M d’afﬁxe z avec $z\neq i$ associe le point M′
d’afﬁxe z′’ telle que :

$z'=\frac{-z^2}{z-i}$

Le but de l’exercice est de construire géométriquement le point M′
connaissant le point M.

1) Un exemple.
On considère un point K d’afﬁxe 1 + i.

a) Placer le point K.

b) Déterminer l’afﬁxe du point K’ image de K par f.
c) Placer le point K′.

2) Des points pour lesquels le problème ne se pose pas.

a) On considère le point L d’afﬁxe $\frac{i}{2}$ .
Déterminer son image L′ par f. Que remarque-t-on ?

b) Un point est dit invariant par f s’il est confondu avec son image.
Démontrer qu’il existe deux points invariants par f dont on déterminera les afﬁxes.

3) Un procédé de construction.

On nomme G l’isobarycentre des points A, M, et M′ , et g l’afﬁxe de G.

a) Vériﬁer l’égalité $g=\frac{1}{3(z-i)}$ .

b) En déduire que si M est un point du cercle de centre A de rayon r, alors G est un point
du cercle de centre O de rayon $\frac{1}{3r}$ .

c) Démontrer que $arg\, g=-(\vec{u},\vec{AM})$ .

d) Sur la feuille annexe, on a marqué un point D sur le cercle de centre A et de rayon $\frac{1}{2}$ .
On nomme D′ l’image de D par f.

Déduire des questions précédentes la construction du point D′

et la réaliser sur la ﬁgure annexe .

Document annexe :

Exercice 21 – Affirmations vraies ou fausses
L’exercice comporte quatre affirmations repérées par les lettres a), b), c) et d). Indiquer pour chacune d’elles si elle est vraie ou fausse.
Soient A le point d’affixe a=1-i et B le point d’affixe b=2i-3 .
A tout point M d’affixe z, avec z différent de b, on associe le point M’ d’affixe:
$Z=\frac{z-1+i,}{z+3-2i}$ .

a) L’ensemble des points M d’affixe z tels que Z soit réel est le segment [AB].
b)Pour tout z différent de -3+2i et de -3-2i, on obtient la forme algébrique de Z par le calcul:
$\frac{(z-1+i)(z+3+2i),}{(z+3-2i)(z+3+2i)}$ .
c)L’ensemble des point M’ d’affixe z tels que M’ soit un point de l’axe des ordonnées et le cercle d’équation $(x+1)^2,+,(y-\frac{1}{2})^2=\frac{25}{4}$ , sauf le point B.
d) Soit z₀ une solution de l’équation $Z=\frac{,z-1+i,}{z+3-2i}=i$ (on admet l’existence d’une telle solution).
Le point M₀d’affixe z₀ est un point de la médiatrice de [AB]

Exercice 22 – Complexes, argument et module
Le plan complexe est muni du repère orthonormal direct (O,u,v) unité graphique 2 cm.
On appelle A et B les points du plan d’affixes respectives a=1 et b=-1
On considère l’application f qui, a tout point M différent du point B, d’affixe z, fait correspondre le point M’ d’affixe z’ définie par $z'=\frac{z-1}{z+1}$ .
1. Déterminer les points invariants de f.
2. a) montrer que, pour tout nombre complexe z différent de -1, .
b) En déduire une relation entre |z'-1| et |z+1| , puis entre arg (z’-1) et arg (z+1), pour tout nombre complexe z diffèrent de -1.
3. Montrer que si M appartient au cercle (C) de centre B et de rayon 2, alors M’ appartient au cercle (C’) de centre A et de rayon 1.
4.Soit le point P d’affixe $P=-2+i\sqrt{3}$ .
a) Déterminer la forme trigonométrique de (p+1)
b) montrer que le point P appartient au cercle (C)

Exercice 23 – Problème.
Le plan complexe est rapporté à un repère orthonormal direct (O; u, v) (unité graphique: 4cm).
On note A, B et C les points d’affixes respectives 2 i, – 1 et i.

On considère l’application f qui, à tout point M diffèrent de A et d’affixe z, associe le point M’ d’affixe z ’ tel que :

$z'=\frac{z+1}{z-2i}$

a. Faire une figure que l’on complétera au cours de l’exercice.

b. Déterminer l’affixe du point C’, image de C par f . Quelle est la nature du quadrilatère ACBC’ ?

c. Montrer que le point C admet un unique antécédent par f , que l’on appellera C ». Quelle est la nature du triangle BCC » ?

2. Donner une interprétation géométrique du module et d’un argument de z ’ (lorsque celui-ci existe).

3.Déterminer en utilisant la question précédente, les ensembles suivants :

a. l’ensemble E_0 des point M dont les images par f ont pour affixe un nombre réel strictement négatif;

b. l’ensemble E_1 des point M dont les images par f ont pour affixe un nombre imaginaire pur non nul;

c. l’ensemble E_2 des points M dont les images appartiennent au cercle de centre O et de rayon 1.

Exercice 24.

Rechercher tous les couples de nombres complexes satisfaisant aux conditions :

$\{{z_1z_2=\frac{1}{2}\atop z_1+2z_2=\sqrt{3}}$ .

Donner la forme trigonométrique de chacun des nombres ainsi obtenus .

Exercice 25 :

Donner la partie réelle et la partie imaginaire de chacun des nombres complexes suivants :

$z_1=1+2i\\z_2=3+i\\z_3=3\\z_4=6i\\z_5=\frac{-i}{2}+\frac{\sqrt{3}}{2}\\z_6=\frac{1}{3}(5+2i)$

Exercice 26 :

On considère les deux nombres complexes suivants :

$z_1=e^{i\frac{\pi}{3}}\,;\,\,z_2=e^{-i\frac{\pi}{4}}$

1. Ecrire z_1 et z_2 sous forme algébrique.

2. Déterminer les écritures sous formes algébrique, exponentielle et trigonométrique de z_1z_2 .

3. En déduire la valeur exacte du cosinus et sinus suivants :

$cos(\frac{\pi}{12})$ et $sin(\frac{\pi}{12})$ .

Exercice 27 :

Déterminer la forme algébrique de chacun des nombres complexes suivants :

$z_1=(1+i)+(-8+4i)\\z_2=(3+i)(5-2i)\\z_3=5i-(3+2i)\\z_4=2(5-i)+3(i-4)\\z_5=(i+2)^2-(3-5i)\\z_6=\,(\,\frac{1}{2}\,+i\frac{\sqrt{3}}{2}\,)^2\\z_7=\frac{5+i}{3+2i}$

Exercice 28 :

Dans le plan complexe, les points A,B et C ont pour affixe respectif

1.Placer les points A, B et C.

2. Déterminer les affixes des points A’ et B’ milieux respectifs des segments [BC] et [AC].

3. déterminer l’affixe du point G défini par $\vec{AG}=\frac{2}{3}\vec{AA'}$

Exercice 29 :

Dans le plan complexe A,B,C et D sont les points d’affixes :

Déterminer les affixes des vecteurs $\vec{AD}$ et $\vec{BC}$ .
Déterminer un argument de $\frac{z_B-z_A}{z_D-z_A}$ .
En déduire la nature du quadrilatère ABCD.

Exercice 30 :

1.a. Résoudre dans $\mathbb{C}$ l’équation $z^2-2\sqrt{3}z+4=0$

b. Donner une forme exponentielle de chacun des solutions.

2. A et M sont les points d’affixes respectives $a=\sqrt{3}+i;m=\sqrt{3}-i$ .

a. Placer les points A et M en indiquant une méthode de construction.

b. On appelle B et C les points d’affixes respectives b=ia et c=ib.

Calculer b et c sous forme algébrique, puis placer B et C.

c. Démontrer que le triangle ABC est rectangle et isocèle.

d. Déterminer l’affixe du point D tel que ABCD soit un carré. Placer ce point D sur la figure.

Exercice 31 :

1)Déterminer la partie réelle et la partie imaginaire de chacun des nombres complexes :

$2+4i;2i;-1-3i;-4;2+\sqrt{3};-\sqrt{5}i$

2)Parmi ces complexes, lesquels sont des réels ?

Lesquels sont imaginaires purs?

Exercice 32 :

Ecrire les nombres complexes sous forme algébrique.

z_8=i^3

z_9=i^4

$z_{10}=(1+i)(1-i)$

$z_{11}=\frac{4+6i}{2}$

$z_{12}=\frac{2-3i}{5}$

$z_{13}=\frac{10+5i}{1-4i^2}$

Exercice 33 :

Déterminer le complexe conjugué de chacun des nombres complexes suivants :

z_2=-4

z_3=7i

$z_6=\frac{4-6i}{2}$

Exercice 34 :

Résoudre dans $\mathbb{C}$ les équations proposées.

On donnera les solutions sous forme algébrique.

Exercice 35 :

Associer chaque complexe au point image qui lui correspond.

z_3=2

z_4=2i

z_5=-2

Exercice 36 :

Associer chaque vecteur à l’affixe qui lui correspond.

z_3=3i

z_4=3-i

z_5=-2

z_6=1-i

Exercice 37 :

1)Déterminer graphiquement les distances OA, OB, OC, OD, OE et OF.

2)En déduire le module de l’affixe de chacun des points A, B, C, D, E et F.

Exercice 38 :

Parmi les écritures proposées ci-dessous, dire lesquelles sont des formes trigonométriques

d’un nombre complexe.

$z_1=\sqrt{3}(cos\frac{\pi}{3}+isin\frac{\pi}{3})$

$z_2=-3(cos\frac{\pi}{4}+isin\frac{\pi}{4})$

$z_3=2(cos(\frac{5\pi}{6})+isin(-\frac{5\pi}{6}))$

Exercice 39 :

Soit le nombre complexe z_1 de module 2 et d’argument $\frac{2\pi}{3}$ et le nombre complexe z_2

de module 4 et d’argument $-\frac{\pi}{6}$ .

1)Déterminer $|\,z_1z_2\,|$ , $|\,\frac{z_1\,}{z_2}\,|$ et $|\,z_1^5\,|$ .

2)Déterminer , $arg(\frac{z_1}{z_2})$ et .

Exercice 40 :

Ecrire sous forme trigonométrique les nombres complexes :

$z_1=e^{i\pi}$ ; $z_2=e^{-i\frac{\pi}{2}}$ ; $z_3=e^{i\frac{2\pi}{3}}$ ; $z_4=e^{-i\frac{5\pi}{6}}$ .

Exercice 41 :

Démontrer que les nombres complexes suivants sont égaux :

$z=5i;z'=\frac{10+5i}{1-2i}$

1. En calculant la différence z’-z.

2. En calculant le quotient $\frac{z'}{z}$ .

Exercice 42 :

Ecrire sous forme algébrique le nombre complexe suivant :

$z=\frac{3+6i}{3-4i}$

Exercice 43 :

On donne .

Ecrire sous forme algébrique les nombres complexes suivants :

$a)\,z_1^2-2z_2\\b)\,z_1z_2^2\\c)\,\frac{z_1}{z_2}\\d)\,\frac{z_1}{z_2}\\,e)\,\frac{1}{z_1}+\frac{1}{z_2}\\f)\,,\frac{1}{z_1^2}+\frac{1}{z_2^2}$

Exercice 44 :

Calculer la somme $S=1+i+i^2+i^3+....+i^{2017}$ .

Exercice 45 :

On pose $j=-\frac{1}{2}+i\frac{\sqrt{3}}{2}$ .

Calculer puis suivant les valeurs du nombre entier naturel n.
Vérifier que .
Calculer la somme $S'=1+j+j^2+j^3+......j^{2017}+j^{2018}$ .

Exercice 46 :

P est le polynôme défini sur $\mathbb{C}$ par .

Vérifier que $P(2+i)=0\,et\,P(2-i)=0$ .

Exercice 47 :

Le plan complexe est rapporté à un repère orthonormé direct d’unité graphique 2 cm.

On considère les points A,B,C et H d’affixes respectives : .

1.a) Placer ces points sur une figure, qui sera complétée au fur et à mesure de l’exercice.

b) Montrer que V est le centre du cercle $\xi$ circonscrit au triangle ABC. Préciser le rayon du cercle $\xi$ .

c) Calculer, sous forme algébrique, le nombre complexe $\frac{b-c}{h-a}$ .

En déduire que les droites (AH) et (BC) sont perpendiculaires.

2. Dans la suite de cet exercice, on admet que H est l’orthocentre du triangle ABC, c’est-à-dire le point d’intersection des hauteurs du triangle ABC.

a. On note G le centre de gravité du triangle ABC.

L’affixe du point G vérifie $g=\frac{1}{3}(a+b+c)$ .

Placer le point G sur la figure.

b) Montrer que le centre de gravité G, l’orthocentre H et le centre du cercle circonscrit au triangle ABC, noté V, sont alignés. Le vérifier sur la figure.

c) On note A’ le milieu de [BC] et K celui de [AH]. Déterminer la nature du quadrilatère KHA’V.

Remarque : dans un triangle, le centre de gravité, l’orthocentre et le centre du cercle circonscrit au triangle sont alignés sur une droite (d) appelée droite d’Euler.

Exercice 48 :

On considère le plan complexe P rapporté à un repère orthonormé $(O\,;\vec{u},\vec{v})$ , et on considère
les points A, B et C distincts situés sur le cercle de centre O et de rayon r.
Les points A’, B’ et C’ sont les images de A, B et C par la rotation de centre O et d’angle $\frac{\pi}{3}$ .
Les points U, V et W sont les milieux des segments [A’B], [B’C], [C’A] ; montrer que le triangle UVW est équilatéral.

Exercice 49 :

Le plan complexe est rapporté à un repère orthonormé $(O\,;\vec{u},\vec{v})$ , et on considère l’application
f du plan complexe dans lui-même qui au point M d’affixe z associe le point M’ d’affixe $f(z)=\frac{z+i\overline{z}}{2}$ .

1. Montrer que l’ensemble (d) des points M dont l’affixe z vérifie f(z) = z est une droite.
2. Montrer que le nombre $\frac{f(z)-z}{1-i}$ est réel.
3. En déduire que M’ appartient à la droite ∆ passant par M et de vecteur directeur $\vec{u}-\vec{v}$
4. Montrer que pour tout nombre complexe z, .
5. Déduire des questions précédentes que M’ est le point d’intersection des deux droites (d) et
∆.
6. Caractériser géométriquement l’application f.

Exercice 50 :

On considère le plan complexe rapporté à un repère orthonormé $(O\,;\vec{u},\vec{v})$ .
On désigne par A le point d’affixe 1 et par C le cercle de centre A et de rayon 1.

PARTIE A :
Soit F le point d’affixe 2, B le point d’affixe $z_B=1+e^{i\frac{\pi}{3}}$ et E le point d’affixe .

Montrer que le point B appartient au cercle C.
Déterminer une mesure en radians de l’angle $\,(\,\vec{AF},\vec{AB}\,\,)$ . Placer le point B.
Déterminer la forme exponentielle des nombres complexes z_B-z_A et z_E-z_A .
En déduire que les points A, B et E sont alignés. Placer le point E.

PARTIE B :
Pour tout nombre complexe z tel que $z\neq\,1$ , on considère les points M et M’ d’affixes respectives z et z’ où .
Pour $z\neq\,0$ et $z\neq\,1$ , donner, à l’aide des points A, M et M’ une interprétation géométrique d’un argument du nombre complexe $\frac{z'-1}{z-1}$ .
En déduire que les points A, M et M’ sont alignés si et seulement si $\frac{z^2}{z-1}$ est un réel.

Exercice 51 :

On considère le plan complexe rapporté à un repère orthonormé $(O\,;\vec{u},\vec{v})$ , et l’application
f du plan complexe dans lui-même qui au point M d’affixe z associe le point M’ d’affixe .
On considère les points B et C d’affixe respectives i et $i\sqrt{3}$ .

1. Calculer les affixes des points images de O, B et C par f.
2. Placer les points B et C et leur image B’ et C’ .
3. L’application f conserve-t-elle l’alignement ?
4. Montrer qu’un point M d’affixe z est invariant par f si et seulement si z vérifie l’équation :
.

5. En déduire que f possède trois points invariants dont on déterminera les affixes.
6. Montrer pour tout z de $\mathbb{C}$ , .

Exercice 52 :

On considère le plan complexe P rapporté à un repère orthonormé $(O\,;\vec{u},\vec{v})$ .
On considère le point M d’affixe z, le point M_1 d’affixe z , le point A d’affixe 2 et le point B d’affixe 1. Soit f l’application de P privé de A dans P, qui à tout point M d’affixe z associe le point M’ d’affixe z’ tel que $z'=\frac{z+4}{\overline{z}-2}$ .
Déterminer les points invariants par f .

4.4/5 - (24914 votes)

×12

L’équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «nombres complexes : exercices de maths en terminale corrigés en PDF.» au format PDF.

Ressources de terminale

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Nombres complexes : exercices de maths en terminale corrigés en PDF.

L’équipe Mathovore

12 Enseignants Titulaires

Ressources de terminale

Cours de terminale

Exercices de terminale

Baccalauréat