Sujet du brevet de mathématiques
Session 2017
Centres étrangers
Exercice 1 : (6 points)
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse. Chaque réponse doit être justifiée.
Affirmation 1 :
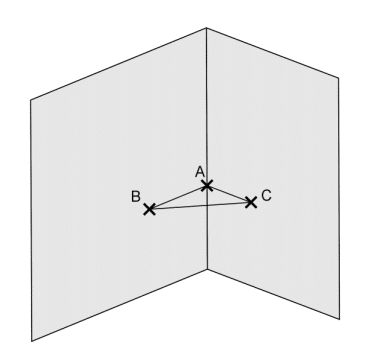
Un menuisier prend les mesures suivantes dans le coin d’un mur à 1 mètre au-dessus du sol pour
construire une étagère ABC :
AB = 65 cm ; AC = 72 cm et BC = 97 cm
Il réfléchit quelques minutes et assure que l’étagère a un angle droit.
Affirmation 2 :
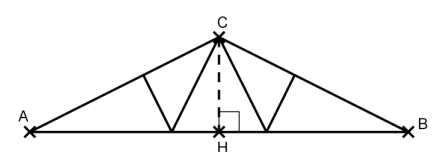
Les normes de construction imposent que la pente d’un toit représentée ici par
l’angle doit avoir une mesure comprise entre 30° et 35°.
Une coupe du toit est représentée ci-contre :
AC = 6 m et AH = 5 m.
H est le milieu de [AB].
Le charpentier affirme que sa construction respecte la norme.
Affirmation 3 :
Un peintre souhaite repeindre les volets d’une maison. Il constate qu’il utilise du pot pour mettre une couche de peinture sur l’intérieur et l’extérieur d’un volet.
Il doit peindre ses 4 paires de volets et mettre sur chaque volet 3 couches de peinture.
Il affirme qu’il lui faut 2 pots de peinture.
Exercice 2 : (7 points)
Partie 1 :
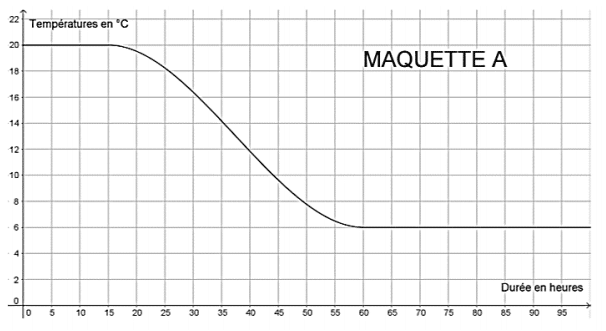
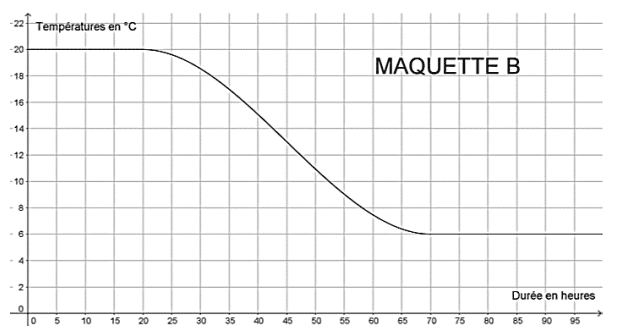
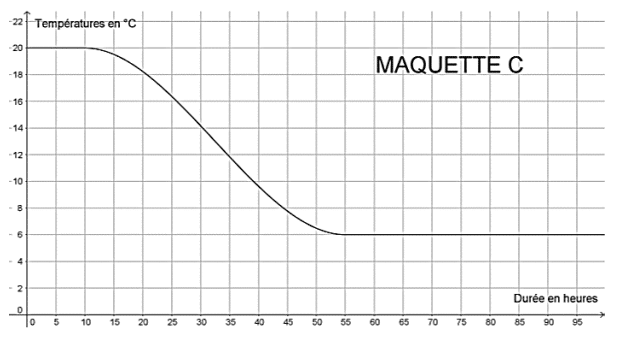
Pour réaliser une étude sur différents isolants, une société réalise 3 maquettes de
maison strictement identiques à l’exception près des isolants qui diffèrent dans chaque
maquette. On place ensuite ces 3 maquettes dans une chambre froide réglée à 6°C.
On réalise un relevé des températures ce qui permet de construire les 3 graphiques
suivants :
1. Quelle était la température des maquettes avant d’être mise dans la chambre froide ?
2. Cette expérience a-t-elle duré plus de 2 jours ? Justifier votre réponse.
3. Quelle est la maquette qui contient l’isolant le plus performant ? Justifier votre réponse.
Partie 2 :
Pour respecter la norme RT2012 des maisons BBC (Bâtiments Basse
Consommation), il faut que la résistance thermique des murs notée soit supérieure
ou égale à 4. Pour calculer cette résistance thermique, on utilise la relation :
où désigne l’épaisseur de l’isolant en mètre et c désigne le coefficient de conductivité
thermique de l’isolant. Ce coefficient permet de connaître la performance de l’isolant.
1. Noa a choisi comme isolant la laine de verre dont le coefficient de conductivité
thermique est : = 0,035. Il souhaite mettre 15 cm de laine de verre sur ses murs.
Sa maison respecte-t-elle la norme RT2012 des maisons BBC ?
2. Camille souhaite obtenir une résistance thermique de 5 ( = 5). Elle a choisi comme
isolant du liège dont le coefficient de conductivité thermique est : = 0,04.
Quelle épaisseur d’isolant doit-elle mettre sur ses murs ?
Exercice 3 : (6 points)
Voici les dimensions de quatre solides :
- Une pyramide de 6 cm de hauteur dont la base est un rectangle de 6 cm de longueur et de 3 cm de largeur.
- Un cylindre de 2 cm de rayon et de 3 cm de hauteur.
- Un cône de 3 cm de rayon et de 3 cm de hauteur.
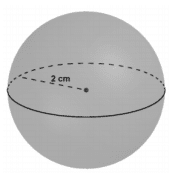
- Une boule de 2 cm de rayon.
1. a) Représenter approximativement les trois premiers solides
comme l’exemple ci-contre.
b) Placer les dimensions données sur les représentations.
2. Classer ces quatre solides dans l’ordre croissant de leur volume.
Exercice 4 : (4 points)
Un fabricant de volets roulants électriques réalise une étude statistique pour connaître
leur fiabilité. Il fait donc fonctionner un échantillon de 500 volets sans s’arrêter, jusqu’à
une panne éventuelle. Il inscrit les résultats dans le tableur ci-dessous :
1. Quelle formule faut-il saisir dans la cellule H2 du tableur pour obtenir le nombre total de volets testés ?
2. Un employé prend au hasard un volet dans cet échantillon.
Quelle est la probabilité que ce volet fonctionne plus de 3000 montées descentes ?
3. Le fabricant juge ses volets fiables si plus de 95 % des volets fonctionnent plus de
1000 montées descentes. Ce lot de volets roulants est-il fiable ? Expliquer votre raisonnement.
Exercice 5 : (6 points)
Sarah vient de faire construire une piscine dont la forme est un pavé droit de 8 m de longueur, 4 m de largeur et 1,80 m de profondeur. Elle souhaite maintenant remplir sa piscine.
Elle y installe donc son tuyau d’arrosage.
Sarah a remarqué qu’avec son tuyau d’arrosage, elle peut remplir un sceau de 10 litres en 18 secondes.
Pour remplir sa piscine, un espace de 20 cm doit être laissé entre la surface de l’eau et le haut de la piscine.
Faut-il plus ou moins d’une journée pour remplir la piscine ? Justifier votre réponse.
Exercice 6 : (9 points)
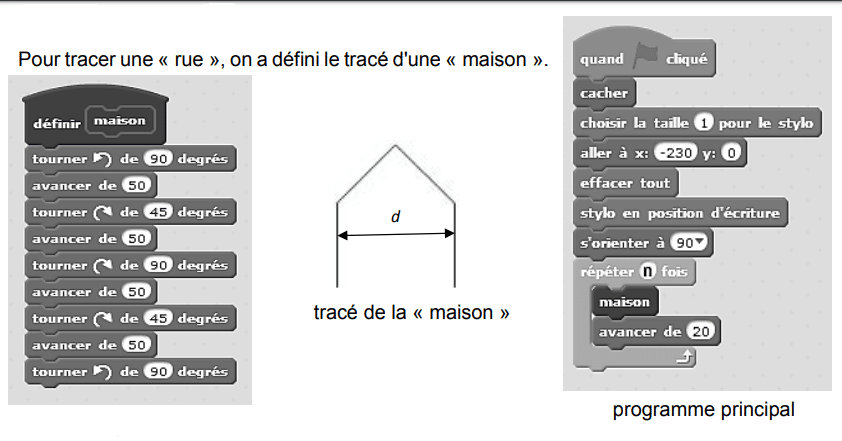
1. Vérifier que d est environ égal à 71 à l’unité près.
2. Un point dans une fenêtre d’exécution de votre programme a son abscisse qui peut varier de – 240 à 240 et son ordonnée qui peut varier de -180 à 180.
Quel est le plus grand nombre entier que l’on peut utiliser dans le programme principal pour que le tracé de la « rue » tienne dans la fenêtre de votre ordinateur où s’exécute le programme ?
Vous pourrez tracer sur votre copie tous les schémas (à main levée ou non) qui auront
permis de répondre à la question précédente et ajouter toutes les informations utiles
(valeurs, codages, traits supplémentaires, noms de points…)
3. Attention, cette question est indépendante des questions précédentes et la « maison » est légèrement différente.
Si on désire rajouter une sortie de cheminée au tracé de la maison pour la rendre plus réaliste, il faut faire un minimum de calculs pour ne pas avoir de surprises.
Exemples :
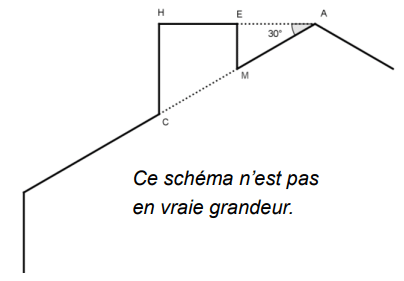
On suppose que :
– les points H, E et A sont alignés ;
– les points C, M et A sont alignés ;
– [CH] et [EM] sont perpendiculaires à [HA] ;
– AM = 16 ;
– MC = 10 ;
– = 30°.
Calculer EM, HC et HE afin de pouvoir obtenir une belle sortie de cheminée.
Exercice 7 : (7 points)
Bob doit refaire le carrelage de sa cuisine dont la forme au sol est un rectangle de 4 m
par 5 m.
Il a choisi son carrelage dans un magasin. Le vendeur lui indique qu’il faut commander
5 % de carrelage en plus pour compenser les pertes dues aux découpes.
Le carrelage choisi se vend dans des paquets permettant de recouvrir 1,12 m² et
chaque paquet coûte 31 €.
1. Montrer que Bob doit commander au moins 21 m² de carrelage.
2. Combien doit-il acheter de paquets de carrelage ?
3. Quel sera le coût de l’achat du carrelage de sa cuisine ?
4. Bob se rend ensuite dans un autre magasin pour acheter le reste de ses matériaux.
Compléter la facture ci-dessous :


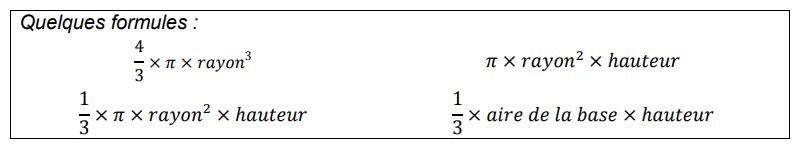






 Mathovore c'est 13 930 037 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 930 037 cours et exercices de maths téléchargés en PDF.