Exercice 1 :
Résoudre l’équation :
Indication : calculer la somme puis remarquer que si x est solution alors x < 0.
Tout d’abord cette somme existe pour .
C’est la somme d’une suite géométrique de raison .
car un dénominateur est non nul.
Exercice 2 :
Calculer la somme suivante :
Indication : regrouper les termes par deux.
Vous pouvez montrer par récurrence que :
donc
Exercice 3 :
Calculer les sommes suivantes :
somme des premiers entiers naturels impairs.
Notons (c’est une suite arithmétique de raison r = 2 )
alors
somme des premiers entiers naturels pairs.
Notons (C’est une suite arithmétique de raison r = 2 )
alors
Exercice 4 :
Soit la suite définie par :
.
1. Calculer
2. La suite
est-elle arithmétique ?
Il semble que la suite soit arithmétique de raison 1.
Exercice 5 :
On considère la suite définie par
.
1. Calculer
2. La suite est-elle arithmétique ? Géométrique ?
calculons les termes suivants par curiosité :
On remarque que cette suite n’est ni arithmétique ni géométrique.
Exercice 6 :
1. Soit la suite définie par
.
Démontrer que est une suite géométrique .
et
ainsi
donc la suite est une suite géométrique de raison q = 2 .
Exercice 7 :
1. Calculer
2. Calculer .
3. Calculer la somme .
Exercice 8 :
1. A l’aide de votre calculatrice, calculer .
Quelle conjecture peut-on faire sur le sens de variation de la suite ? Pour une éventuelle limite ?
La suite est décroissante vers 0.
2. Démontrer que pour tout n non nul,
.
Nous avons :
et utilisons l’identité remarquable
.
3. En déduire le sens de variation de la suite .
or donc en multipliant l’inégalité par
, nous obtenons :
Conclusion : la suite est décroissante .
4. En utilisant le résultat de la question 2., montrer que, pour tout entier naturel n non nul,
.
Nous avons
5. En déduire que la suite est convergente et préciser sa limite.
Nous avons donc :
et
donc d’après le théorème des gendarmes , on en conclue que
Exercice 9 :
La suite est arithmétique de raison
.
On sait que et
.
1. Calculer la raison et
Pour le terme
2. Calculer la somme .
D’après le cours :
donc :
Conclusion :
Exercice 10 :
On additionne deux fois cette somme :
1+2+3+4+5+……+998+999
999+998+……..+5+4+3+2+1
—————————————
1000+1000+1000+……….+1000 Il y a 999 fois 1000
donc
Exercice 11 :
On considère la suite définie pour tout entier naturel non nul par la relation :
.
1. Démontrer que la suite est arithmétique de raison r que l’on précisera. Préciser son sens de variation.
c’est une suite arithmétique de raison 3 et elle est donc croissante puisque
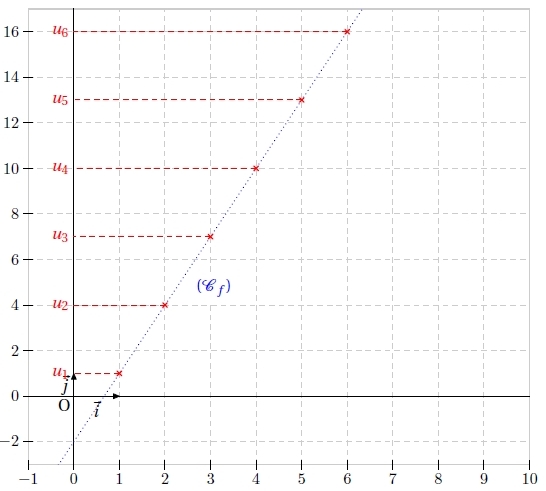
2. Représenter graphiquement la suite .
On se limitera aux cinq ou six premiers termes.
C’est la somme d’une suite géométrique de raison q = – 2.
Exercice 13 :
1. A quelle page en est Jean ?
Notons n la page où en est Jean.
Nous avons
Nous sommes amenés à résoudre l’équation suivante :
Calculons la valeur du discriminant :
Le discriminant est strictement positif, il y a donc deux racines réelles distinctes.
Conclusion : Jean a lu 26 pages, il en est donc à la 27ème page.
2. Combien de pages comporte ce livre ?
Nous avons
Calculons la valeur du discriminant :
Le discriminant est strictement positif, il y a donc deux racines réelles disctinctes .
Conclusion : ce livre a 40 pages .
Remarque : on supposera que le livre commence à la page n° 1.
Exercice 14 :
Déterminer un nombre x tel que les trois nombres 25, x et 16 soient trois termes consécutifs d’une suite géométrique de raison négative.
Nous avons et
donc
En utilisant le produit en croix :
Il y a deux possibilités :
soit
Or la raison q est négative donc x étant le second des trois termes, il est forcément négatif.
Conclusion : x = – 20 .
Exercice 15 :
Un étudiant loue une chambre pour 3 ans.
On lui propose deux type de bail :
1er contrat : un loyer de 200€ pour le premier mois puis une augmentation de 5 € par mois jusqu’à la fin du bail.
2ème contrat : un loyer de 200 € pour le premier mois puis une augmentation de 2 % par mois jusqu’à la fin du bail.
1. Calculer, pour chacun des deux contrats, le loyer du deuxième mois puis celui du troisième mois.
et
2. Calculer, pour chacun des deux contrats, le loyer du dernier mois, c’est-à-dire du 36ème mois.
et
3. Quel est le contrat globalement le plus avantageux pour un bail de 3 ans ? Justifier à l’aide de calculs.
Vocabulaire : un bail est un contrat de location.
Le deuxième est le plus avantageux de 35 euros.
Exercice 16 :
1. ABC est un triangle rectangle.
Son plus petit côté est 1 et les longueurs de ses côtés sont trois termes
consécutifs d’une suite arithmétique.
Déterminer ces longueurs.
Calculons la valeur du discriminant :
Le discriminant est strictement positif donc il existe deux racines réelles distinctes.
Donc
et
Conclusion : les trois nombres consécutifs sont .
2. ABC est un triangle rectangle.
Son plus petit côté est 1 et les longueurs de ses côtés sont trois termes
consécutifs d’une suite géométrique.
Déterminer ces longueurs.
Calculons la valeur du discriminant :
donc
ne convient pas car la raison serait négative.
Ainsi
Conclusion : les trois nombres sont .
Exercice 17 :
On considère la suite définie par récurrence par :
1. Calculer
2. Résoudre l’équation du second degré suivante : .
Calculons la valeur du discriminant :
, il y a donc deux racines réelles distinctes.
3. Déterminer deux réels A et B tels que : .
Effectuons la soustraction de la deuxième ligne et de la première.
Conclusion :
Remarque : il faudrait montrer cette égalité par récurrence…
4. En déduire
Exercice 18 :
Déterminer la limite de la suite définie par :
pour tout
.
car les fonctions cos et sin sont bornées par -1 et 1.
Exercice 19 :
On considère la suite définie par récurrence par :
1. Calculer
2. Démontrer par récurrence que pour tout
Soit la propriété de récurrence :
P(n) : » pour ,
«
Initialisation :
car
.
Hérédité :
supposons qu’il existe n tel que P(n) soit vraie.
Nous avons donc
car la fonction inverse est décroissante sur
.
donc
ainsi la propriété reste vraie au rang n+1
Conclusion :
Donc
ainsi
Exercice 20 :
Calculer la valeur exacte des nombres suivants :
c’est la somme des premiers termes d’une suite géométrique de raison et de premier terme
C’est la somme d’une suite arithmétique de raison 3 avec
Exercice 21 :
Indication : revenir à la définition d’une suite arithmétique.
On considère u(n) une suite arithmétique de raison r.
1°) Justifier que u(3) = u(2) + r et que u(4) = u(3) + r
En déduire que
2°) Montrer que .
3°) Quelle relation peut-on écrire entre u(7) , u(2) et r ? Justifier.
4°) On suppose dans cette question que u(0) = 4 et r = 2.
Calculer u(5) .
Donner sans démonstration la valeur de u(100)
Exercice 22 :
On définit une suite (un) par : pour tout entier n.
On a par exemple, en remplaçant n par 10 : u10 = 17 243 – 8 x 10 = 17 163
1°) Calculer u0 =17243 ; u1=17235 ; u1990=1323 ; u1991=1315 ; u1992=1307 .
2°) Calculer u1 – u0 =-8 ; u1991 – u1990=-8 ; u1992 – u1991 =-8
3°) En remplaçant n par n+1 dans l’expression de un montrer que
pour tout entier n : un+1 = 17 235 – 8n
En déduire que, pour tout entier n : un+1 – un = -8
4°) En utilisant la relation un+1 – un = -8, c’est-à-dire un+1 = un – 8 compléter le tableau suivant.
La suite (un) est-elle une suite décroissante ?
|
n |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
|
un |
1 323 |
|
|
|
|
|
|
|
|
|
|
5°) Représenter graphiquement la suite (un) lorsque n varie de 1990 à 2000.
Exercice 23 :
On donne, dans le tableau suivant, le nombre d’inscrits sur la liste électorale d’une petite commune pour les années de 1990 à 2000.
|
Année |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
|
Nombre d’inscrits |
1323 |
1313 |
1304 |
1297 |
1288 |
1289 |
1281 |
1271 |
1258 |
1248 |
1243 |
1°) On note Pn le nombre d’inscrits sur la liste électorale pour l’année n.
Donner la valeur de P1992=1304 et P1998=1258
2°) Calculer P1994 – P1993. Que représente ce nombre ?
Calculer P1995 – P1994. Que représente ce nombre ?
3°) Peut-on dire que la suite des nombres Pn est une suite décroissante lorsque n varie de 1990 à 2000 ?
4°) Représenter graphiquement la suite (Pn).
Exercice 24 :
Indication :
Nécessaire au calcul :
Le montant, qu’on notera m .
Le taux d’intérêt, qu’on notera i .
Le nombre de périodes, qu’on notera n .
Formule du calcul des intérêts composés :
m * (1+i)n
On dispose d’un capital de €.
Le 1er janvier 2000, on place ce capital sur un compte à intérêts composés de 3 % par an.
1. Calculer le capital obtenu au bout d’un an.
2. Calculer le capital obtenu au bout de 7 ans.
De quel pourcentage a augmenté le capital pendant ces 7 années ?
3. Combien d’années faut-il laisser cet argent sur le compte afin d’avoir un capital d’au moins 2 000 € ?
Exercice 25 :
Indication : une réduction de 1,14% correspond à un coefficient multiplicateur
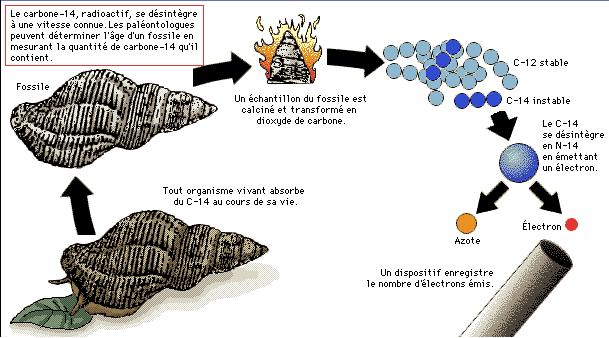
Les rayons cosmiques produisent continuellement dans l’atmosphère du carbone 14 qui est un élément radioactif.
Durant leur vie, les tissus animaux et végétaux contiennent la même proportion de carbone 14 que l’atmosphère.
Cette proportion décroît après la mort du tissu de 1,14 % en 100 ans.
1. Déterminer les pourcentages de la proportion initiale de carbone 14 contenu dans le tissu au bout de 1 000 ans, 2 000 ans et 10 000 ans.
2. Exprimer le pourcentage de la proportion initiale de carbone 14 contenu dans le tissu au bout de annéees.
3. Un fossile ne contient plus que 10 % de ce qu’il devait contenir en carbone 14.
Donner une estimation de son âge.
Exercice 26 :
En quelle année était-ce ?
Nous obtenons une suite géométrique de raison q = 2.
=29,9
Conclusion : Le trentième mois.
Rémunération dans une entreprise, exercices corrigés de mathématiques en première S sur les suites numériques.
Exercice 27 :
1°) Dans le cas de la rémunération de type 1, on note u(0) le salaire mensuel initial, et u(n) le salaire mensuel après n années. Donner les valeurs de u(0), u(1), u(2).
2°) Dans le cas de la rémunération de type 2, on note v(0) le salaire mensuel initial, et v(n) le salaire mensuel après n années. Donner les valeurs de v(0), v(1), v(2).
3°) Donner une expression générale de u(n) et v(n) en fonction de n. Calculer u(5) et v(5) ; u(8) et v(8).
4°) Le nouvel employé compte rester 10 ans dans l’entreprise. Quelle est la rémunération la plus avantageuse ?
Exercice 28 :
Indication : utiliser le coefficient multiplicateur pour une réduction de 12 % qui est
Un village avait 3123 habitants en 1995. Le nombre d’habitants diminue de 12% tous les ans.
On note P(n) le nombre d’habitants du village pour l’année n.
1°) Donner les valeurs de P(1995) et P(1996). (on arrondira à l’entier le plus proche)
2°) Justifier que la suite P(n) est une suite géométrique et donner sa raison.
Exercice 29 :
Indication : utiliser le coefficient multiplicateur pour une réduction de 12 % qui est
Un village avait 3123 habitants en 1995. Le nombre d’habitants diminue de 12% tous les ans.
On note P(n) le nombre d’habitants du village pour l’année n.
1°) Donner les valeurs de P(1995) et P(1996). (on arrondira à l’entier le plus proche)
2°) Justifier que la suite P(n) est une suite géométrique et donner sa raison.
3°) Calculer P(2001). (on arrondira à l’entier le plus proche)
4°) En quelle année le nombre d’habitants aura-t-il diminué des deux tiers par rapport à 1995 ?
5°) Représenter graphiquement la suite P(n) pour n variant de 1995 à 2005.
Exercice 30 :
Un capital de 12 618 euros est placé le 01/01/2000 avec un taux d’intérêt annuel de 6,3%.
Tous les ans les intérêts sont cumulés au capital.
On note C(0) le capital correspondant au 1er janvier de l’année 2000. On a donc C(0) = 12 618.
On note, pour tout entier n, C(n) le capital correspondant au 1er janvier de l’année 2000+n.
1°) Calculer C(1), C(2), C(3). (on arrondira les résultats au centime d’euro près)
2°) Démontrer que pour tout entier n on a C(n+1) = C(n) x 1,063.
3°) Compléter le tableau suivant (on arrondira les résultats au centime d’euro près)
|
Rang n de l’année |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Capital C(n) |
12 618 |
|
|
|
|
|
|
|
|
|
|
4°) Représenter graphiquement la suite C(n).
Exercice 31 :
Soit une suite arithmétique et de raison
et telle que
.
Calculer la valeur du premier terme .
Nous avons
Exercice 32 :
On considère la suite définie par
.
1. Calculer
2. Justifier que la suite est une suite arithmétique dont on précisera la raison.
Nous avons ( par définition)
Donc c’est une suite arithmétique de raison .
3. Que vaut ?
Exercice 33 :
On considère la suite définie par
.
1. Calculer
2. La suite est-elle arithmétique ? Si oui, préciser la raison.
Soit :
Conclusion : c’est une suite arithmétique de raison r = 2 .
3. Que vaut ?
4. Calculer la somme .
en fait :
Exercice 34 :
On considère définie par
.
1. Calculer
2. Démontrer que est une suite arithmétique dont on précisera la raison.
Soit ,
Conclusion : la suite est une suite arithmétique de raison r = – 2.
3. Que vaut ?
Calculer .
Exercice 35 :
1/ a) Le pied de triodule occupe, au début de 1801, une surface de .
À la fin de l’année 1801, il a occupé une surface supplémentaire de , donc il occupe maintenant une surface totale de
.
b) En 1802, le pied de triodule ne produit pas de nouvelle graine, donc il ne s’étend pas au-delà de sa surface actuelle de .
c) À la fin de l’année 1802, le pied de triodule occupe toujours une surface de $2m^2$, comme il ne produit pas de nouvelle graine.
2/ En utilisant un tableur avec les instructions donnés, on peut obtenir :
| Année | Surface occupée (en m²) |
|——-|————————|
| 1801 | 2 |
| 1802 | 2 |
| 1803 | 3 |
| 1804 | 4 |
| … | … |
| 2000 | 199 |
3/ a) On a (la surface occupée à la fin de l’année 1800 est 1, car c’est la surface initiale occupée par la première graine de triodule).
En 1801, on a , car le premier pied de triodule va occuper une surface de 2m² et produire une nouvelle graine qui germera à la fin de l’année.
En 1802, on a , car le premier pied de triodule occupe toujours une surface de 2m², et les deux autres pieds vont chacun occuper une surface de 2m² à la fin de l’année.
b) À la fin de l’année 1800+n, le premier pied de triodule aura occupé une surface de $n$ m².
c) On peut facilement vérifier que , car chaque graine de triodule produite correspond à une nouvelle surface de 1m², et le nombre de graines produites est égal au nombre d’années écoulées depuis l’arrivée de la première graine en 1800.
d) Au bout de 20 ans (soit en 1820), on auram².
e) On cherche la plus petite valeur de $n$ telle que . On a :
Il faut donc résoudre l’équation .
En développant cette inéquation, on obtient :
Les solutions de cette équation sont :
Comme $n$ doit être un entier positif, on a .
Ainsi, la surface totale des pieds de triodule dépassera 500m² en 1832 (soit à la fin de l’année 32, avec une surface occupée de m²).
Exercice 36 :
Etudier la nature des suites ci-dessous :
a) pour tout entier naturel n, .
donc la suite
est décroissante .
b) pour tout entier naturel n, .
donc est décroissant et
.
Exercice 37 :
On note la suite définie par :
1. Calculer
2. Exprimer en fonction de
.
3. Exprimer en fonction de
.
4. En déduire l’expression de , en fonction de
(On ne démontrera pas l’égalité trouvée).
5. Calculer .







 Mathovore c'est 13 929 601 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 929 601 cours et exercices de maths téléchargés en PDF.