Un sujet du brevet de maths 2016 qui est un devoir en commun blanc afin de permettre aux élèves de réviser le brevet des collèges 2016 en mathématiques.
Toutes les réponses doivent être justifiées.
Pour chaque question, si le travail n’est pas terminé, laisser tout de même une trace de la recherche.
Elle sera prise en compte dans la notation.
Exercice 1 : ( 3 points)
Dans une école de ski, il y a 2 346 enfants inscrits et 966 adultes pour la période du 18 au 25 mars 2015.
Les moniteurs souhaitent faire des groupes tous identiques composés d’adultes et d’enfants.
Tous les inscrits doivent appartenir à un groupe et à un seul.
- Quel est le nombre maximum de groupes qu’ils peuvent faire ? Expliquer.
- Calculer le nombre d’enfants et d’adultes dans chaque groupe.
Exercice 2 : (4,5 points)
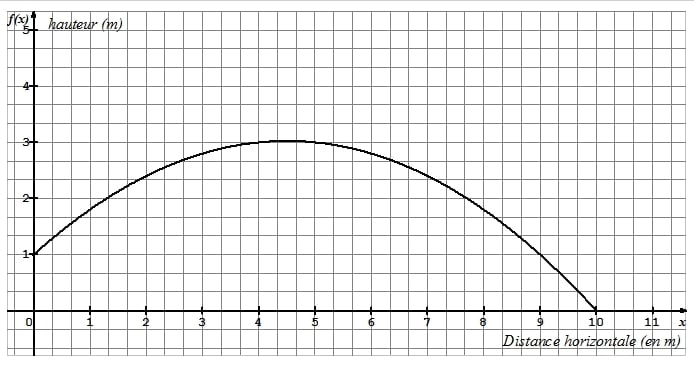
Pour son anniversaire, Vanessa a reçu un coffret de tir à l’arc.
Elle tire une flèche. La trajectoire de la pointe de cette flèche est représentée ci-dessous.
La courbe donne la hauteur (en mètres) en fonction de la distance horizontale ( en mètres )
parcourue par la flèche.
1) Dans cette partie, les réponses seront données grâce à des lectures graphiques.
a) De quelle hauteur la flèche est-elle tirée ?
b) À quelle distance de Vanessa la flèche retombe-t-elle au sol ?
c) Déterminer l’image de 
par la fonction f.
d) Déterminer le(ou les) antécédent(s) de 1 par la fonction f .
2) Dans cette partie, les réponses seront justifiées par des calculs :
La courbe ci-dessus représente la fonction f définie par f (x) = −0,1x2+0,9x +1.
a) Calculer f (4,5).
b) La flèche peut-elle s’élever à plus de 3m de hauteur ?
Exercice 3 : (3,5 points)
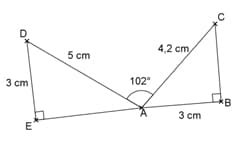
La figure ci- dessous est dessinée à main levée. Elle n’est pas exacte.
Calculer la mesure de l’angle arrondie au degré près.
Les points E, A et B sont-ils alignés ? Justifiez votre réponse.
Exercice 4 : (3,5 points)
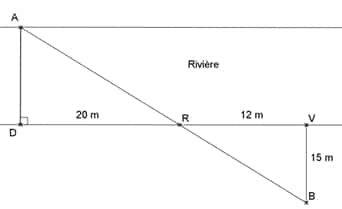
Joachim doit traverser une rivière avec un groupe d’amis.
Il souhaite installer une corde afin que les personnes peu rassurées puissent se tenir.
Il veut connaître la largeur de la rivière à cet endroit (nommé D) pour déterminer si la corde dont il dispose est assez longue. Pour cela il a repéré un arbre (nommé A) sur l’autre rive.
Il parcourt 20 mètres sur la rive rectiligne où il se situe et trouve un nouveau repère : un rocher (nommé R).
Ensuite il poursuit sur 12 mètres et s’éloigne alors de la rivière, à angle droit, jusqu’à ce que le rocher
soit aligné avec l’arbre depuis son point d’observation (nommé B).
Il parcourt pour cela 15 mètres. Il est alors satisfait : il pense que sa corde d’une longueur de 30 mètres
est assez longue pour qu’il puisse l’installer entre les points D et A.
A l’aide de la figure, confirmer sa décision.
La figure n’est pas à l’échelle.
Exercice 5 : ( 4 points)
Quatre affirmations sont énoncées ci-dessous.
Pour chacune, indiquer si elle est vraie ou fausse en justifiant la réponse.
Exercice 6 : (2,5 points)
Valentin a inventé un sujet d’exercice. Il commence ainsi :
« ABC est un triangle rectangle tel que AB = 4 cm, AC = 8 cm et BC = 7 cm … »
Sa camarade Nadia, très forte en calcul mental, l’interrompt aussitôt et lui dit :
« On ne pourra pas faire ton exercice car il y a une erreur dès le début ! Je n’ai même pas besoin
de commencer à faire la figure. »
Expliquer comment Nadia peut-elle être aussi sûre d’elle.
Exercice 7 : (4 points)
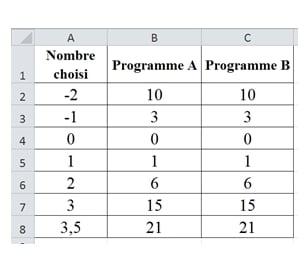
On considère ces deux programmes de calcul :
1) a) Montrer que si on applique le programme A au nombre 10, le résultat est 190.
b) Appliquer le programme B au nombre 10.
2) On a utilisé un tableur pour calculer des résultats de ces deux programmes. Ci-dessous les résultats obtenus.
a) Quelle formule a-t-on saisie dans la cellule C2 puis recopiée vers le bas ?
b) Quelle conjecture peut-on faire à la lecture de ce tableau ?
c) Prouver cette conjecture.
Exercice 8 : (4 points)
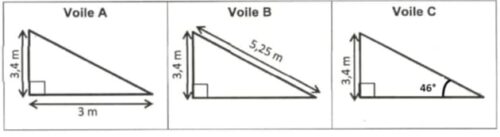
Pour son confort, Elise souhaite installer une voile d’ombrage triangulaire dans son jardin.
L’aire de celle-ci doit être de 6 m² au minimum.
Parmi les trois voiles suivantes, quelle(s) sont celle(s) qui pourraient convenir ?
Les schémas ci-dessous ne sont pas à l’échelle.
Signaler une erreur
Aidez-nous à améliorer cette page en signalant une erreur
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2016 : sujet blanc» au format PDF.
Réviser les leçons et les exercices avec nos Q.C.M :
D'autres utilitaires pour progresser en autonomie :
