Brevet de maths 2023 : sujet blanc des collèges. pour réviser.

Sommaire de cette fiche

1 Exercice 1 : (5 pts)
2 Exercice 2 : (5 pts)
3 Exercice 3 : (4 pts)
4 Exercice 4 : (4 pts)
5 Exercice 5 : (4 pts)
6 Exercice 6 : (4 pts)
7 Exercice 7 : (4 pts)
8 Exercice 8 : (3 pts)
9 Exercice 9 : (3 pts)

Le brevet de maths 2023 avec un sujet blanc pour le DNB des collèges en troisième (3ème).Ce sujet contient 9 exercices indépendants.

La calculatrice est autorisée. Durée de l’épreuve : 2 h. Notation sur 40.
La clarté de la présentation, la qualité de la rédaction comptent sur 4 points dans la note finale.
Toutes les réponses doivent être soigneusement justifiées sauf indications contraires.

Exercice 1 : (5 pts)

1. Calculer les expressions A et B et donner le résultat sous la forme d’une fraction
irréductible :

$A=\frac{\frac{-1}{4}+6}{\frac{7}{10}-6}$ $B=1+\frac{8}{7}\times ,\frac{35}{9}$

2. Calculer l’expression C et donner l’écriture scientifique du résultat :

$C=\frac{10^3\times ,10^{-6}\times ,2700\times ,10^5}{24000\times ,,(,10^{-5},,)^2}$

3. Développer et réduire :

Exercice 2 : (5 pts)

On donne le programme de calcul ci-dessous :

Programme :
– Choisir un nombre
– Lui ajouter 2
– Calculer le carré de cette somme.
– Soustraire 9 au résultat obtenu.

1. On choisit 3 comme nombre de départ.
Montrer que le résultat du programme est 16.
2. On choisit (-1) comme nombre de départ.
Calculer le résultat du programme.
3. On appelle x le nombre de départ. Ecrire le résultat du programme de calcul en fonction de x.
4. Factoriser cette expression.
5. Quel(s) nombre(s) faut-il choisir au départ pour que le résultat du programme soit nul ?

Exercice 3 : (4 pts)

Les informations suivantes concernent les salaires des hommes et des femmes d’une même entreprise :

Salaires de chaque femme :
1 200 € ; 1 230 € ; 1 250 € ; 1 310 € ; 1 370 € ; 1 400 € ; 1 440 € ; 1 500 € ; 1 700 € ; 2 100 €

Salaires des hommes :
Effectif total : 20
Moyenne : 1 769 €
Etendue : 2 400 €
Médiane : 2 000 €
Les salaires des hommes sont tous différents.

1. Comparer le salaire moyen des hommes et celui des femmes.
2. On tire au sort une personne dans l’entreprise. Quelle est la probabilité que ce soit une femme ?
3. Le plus bas salaire de l’entreprise est de 1 000 €. Quel salaire est le plus élevé ?
4. Dans cette entreprise combien de personnes gagnent plus de 2 000 € ?

Exercice 4 : (4 pts)

Dans une urne il y a 1 boule jaune (J), 4 boules bleues (B) et 2 boules rouges (R), indiscernables au toucher. On tire successivement, deux boules, avec remise (on remet la première boule avant de prendre la deuxième).
1. Construire l’arbre des possibles décrivant l’expérience aléatoire ; placer les probabilités sur chaque branche.
2. Quelle est la probabilité que la première boule soit rouge et la deuxième boule soit bleue ?
3. On considère l’évènement A : » la 2ème boule est jaune’’
a. Quelles sont toutes les issues possibles ?
b. En déduire la probabilité de l’évènement A.

Exercice 5 : (4 pts)

1. Construire un triangle ABC tel que : AB = 10,5 cm, AC = 6,3 cm et BC = 8,4cm.
Placer le point E sur la droite (AB) tel que : E $\notin$ [AB] et BE = 4,5 cm.
Tracer la perpendiculaire à la droite (BC) passant par le point E. Elle coupe la droite (BC) en F.
Placer F.
2. Démontrer que le triangle ABC est rectangle.
3. Calculer la longueur BF.
4. Placer les points M et N tels que : M $\in$ [AB], N $\in$ [BC], BM = 5cm et BN = 4cm.
Les droites (MN) et (AC) sont-elles parallèles ? Justifier la réponse.

Exercice 6 : (4 pts)

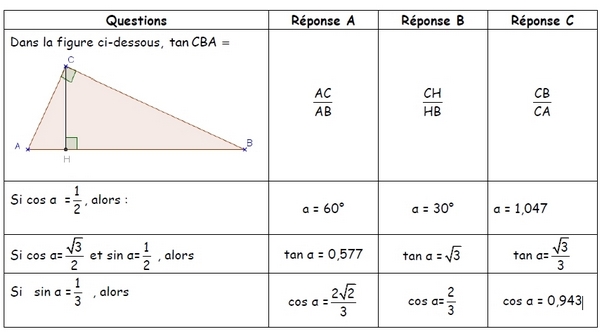
Cet exercice est un questionnaire à choix multiples. Pour chaque question, une seule réponse est
exacte. L’absence de réponse ou une réponse fausse ne retire aucun point.
Entourer la réponse choisie. Aucune justification n’est demandée .

Exercice 7 : (4 pts)

On a utilisé un tableur pour calculer les images de différentes valeurs de x par une fonction f
et par une autre fonction g. Une copie de l’écran obtenue est donnée ci-dessous :

1. Quelle est l’image de -3 par f ?
2. Calculer f(7).
3. Donner l’expression de f (x).
4. On sait que g (x) = x² + 4. Une formule a été saisie dans la cellule B3 et recopiée ensuite vers
la droite pour compléter la plage de cellules C3: H3. Quelle est cette formule ?

Exercice 8 : (3 pts)

1. Rendre irréductible le quotient $\frac{126}{175}$ en utilisant un calcul de PGCD.
Un commerçant possède 175 boules de Noël rouges et 126 boules bleues. Il a choisi de
confectionner des sachets tous identiques. Il voudrait en avoir le plus grand nombre en utilisant
toutes les boules.
2. Combien de sachets pourra-t-il réaliser ?
3. Combien de boules de chaque couleur y aura-t-il dans chaque sachet ?

Exercice 9 : (3 pts)

Avant l’épreuve, un plan a été remis aux élèves participant à la course.
Il est représenté par la figure ci-dessous :

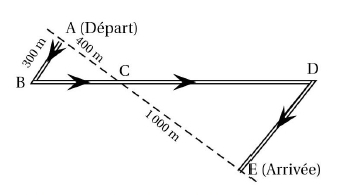
On convient que :
– les droites (AE) et (BD) se coupent en C.
– les droites (AB) et (DE) sont parallèles.
– ABC est un triangle rectangle en A.
Calculer la longueur réelle du parcours ABCDE.

Si le travail n’est pas terminé laissez tout de même une trace de recherche. Elle sera prise en compte dans la notation.

Consulter le corrigé en ligne

4.9/5 - (13 votes)