MATHÉMATIQUES
Série S
Enseignement Obligatoire – Coefficient 7
Durée de l’épreuve : 4 heures
Exercice 1 : Commun à tous les candidats (5 points)
Dans cet exercice et sauf mention contraire, les résultats seront arrondis à .
Une usine fabrique des tubes.
Partie A
Les questions 1 et 2 sont indépendantes.
On s’intéresse à deux types de tubes, appelés tubes de type 1 et tubes de type 2.
1. Un tube de type 1 est accepté au contrôle si son épaisseur est comprise entre 1,35 millimètres et 1,65 millimètres.
a. On désigne par X la variable aléatoire qui, à chaque tube de type 1 prélevé au hasard dans la production d’une journée, associe son épaisseur exprimée en millimètres. On suppose que la variable aléatoire X suit la loi normale d’espérance 1,5 et d’écart-type 0,07.
On prélève au hasard un tube de type 1 dans la production de la journée. Calculer la probabilité que le tube soit accepté au contrôle.
b. L’entreprise désire améliorer la qualité de la production des tubes de type 1. Pour cela, on modifie le réglage des machines produisant ces tubes.
On note X1 la variable aléatoire qui, à chaque tube de type 1 prélevé dans la production issue de la machine modifiée, associe son épaisseur. On suppose que la variable aléatoire X1 suit une loi normale d’espérance 1,5 et d’écart-type σ1.
Un tube de type 1 est prélevé au hasard dans la production issue de la machine modifiée. Déterminer une valeur approchée à 10−3 près de σ1 pour que la probabilité que ce tube soit accepté au contrôle soit égale à 0,98. (On pourra utiliser la variable aléatoire Z définie par qui suit la loi normale centrée réduite.)
2. Une machine produit des tubes de type 2. Un tube de type 2 est dit « conforme pour la longueur » lorsque celle-ci, en millimètres, appartient à l’intervalle [298 ; 302]. Le cahier des charges établit que, dans la production de tubes de type 2, une proportion de 2 % de tubes non «conformes pour la longueur » est acceptable.
On souhaite décider si la machine de production doit être révisée. Pour cela, on prélève au hasard dans la production de tubes de type 2 un échantillon de 250 tubes dans lequel 10 tubes se révèlent être non « conformes pour la longueur ».
a. Donner un intervalle de fluctuation asymptotique à 95 % de la fréquence des tubes non « conformes pour la longueur » dans un échantillon de 250 tubes.
b. Décide-t-on de réviser la machine ? Justifier la réponse.
Partie B
Des erreurs de réglage dans la chaîne de production peuvent affecter l’épaisseur ou la longueur des tubes de type 2. Une étude menée sur la production a permis de constater que :
– 96 % des tubes de type 2 ont une épaisseur conforme ;
– parmi les tubes de type 2 qui ont une épaisseur conforme, 95 % ont une longueur conforme ;
– 3,6 % des tubes de type 2 ont une épaisseur non conforme et une longueur conforme.
On choisit un tube de type 2 au hasard dans la production et on considère les événements :
– : « l’épaisseur du tube est conforme » ;
– : « la longueur du tube est conforme ».
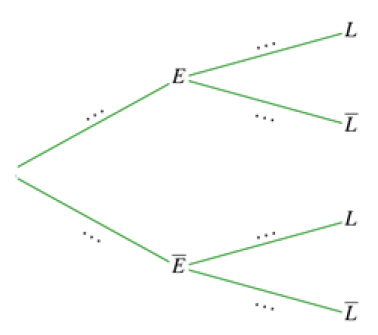
On modélise l’expérience aléatoire par un arbre pondéré :
1. Recopier et compléter entièrement cet arbre.
2. Montrer que la probabilité de l’événement est égale à 0,948.
Exercice 2 : Commun à tous les candidats (4 points)
Le plan complexe est muni d’un repère orthonormé direct .
Dans ce qui suit, désigne un nombre complexe.
Pour chacune des affirmations ci-dessous, indiquer sur la copie si elle est vraie ou si elle est fausse. Justifier. Toute réponse non justifiée ne rapporte aucun point.
Affirmation 1 : L’équation −i=i(+1) a pour solution .
Affirmation 2 : Pour tout réel , le nombre complexe
admet pour forme exponentielle
.
Affirmation 3 : Un point M d’affixe z tel que |−i|=|+1| appartient à la droite d’équation =−.
Affirmation 4 : L’équation admet une solution réelle.
Exercice 3 : Commun à tous les candidats (6 points)
Partie A : établir une inégalité
Sur l’intervalle , on définit la fonction par
.
1. Étudier le sens de variation de la fonction sur l’intervalle .
2. En déduire que pour tout [,
.
Partie B : application à l’étude d’une suite
On pose et pour tout entier naturel ,
. On admet que la suite de terme général
est bien définie.
1. Calculer une valeur approchée à près de
.
2. a. Démontrer par récurrence que pour tout entier naturel , .
b. Démontrer que la suite est décroissante, et en déduire que pour tout entier naturel , ≤1 .
c. Montrer que la suite est convergente.
3. On note la limite de la suite et on admet que
où est la fonction définie dans la partie A. En déduire la valeur de .
4. a. Écrire un algorithme qui, pour un entier naturel donné, permet de déterminer le plus petit rang N à partir duquel tous les termes de la suite sont inférieurs à
.
b. Déterminer le plus petit entier naturel à partir duquel tous les termes de la suite sont inférieurs à
.
Exercice 4 : Candidats n’ayant pas suivi l’enseignement de spécialité (5 points)
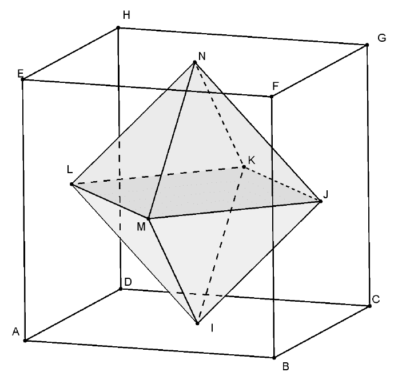
On relie les centres de chaque face d’un cube ABCDEFGH pour former un solide IJKLMN comme sur la figure ci-dessous.
Plus précisément, les points I, J, K, L M et N sont les centres respectifs des faces carrées
ABCD, BCGF , CDHG, ADHE, ABFE et EFGH (donc les milieux des diagonales de ces carrés).
1. Sans utiliser de repère (et donc de coordonnées) dans le raisonnement mené, justifier que les droites
(IN) et (ML) sont orthogonales.
Dans la suite, on considère le repère orthonormé dans lequel, par exemple, le point N a pour coordonnées
.
2. a. Donner les coordonnées des vecteurs et
.
b. En déduire que les droites (NC) et (ML) sont orthogonales.
c. Déduire des questions précédentes une équation cartésienne du plan (NCI) .
3. a. Montrer qu’une équation cartésienne du plan (NJM) est : .
b. La droite (DF) est-elle perpendiculaire au plan (NJM) ? Justifier.
c. Montrer que l’intersection des plans (NJM) et (NCI) est une droite dont on donnera un point et un vecteur directeur. Nommer la droite ainsi obtenue en utilisant deux points de la figure.





 Mathovore c'est 13 931 817 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 931 817 cours et exercices de maths téléchargés en PDF.